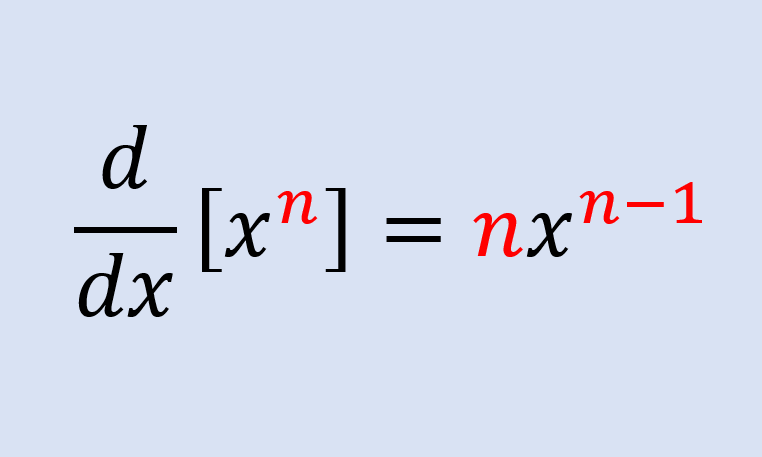Proofs of the Power Rule of Derivatives

What is the Power Rule?

The power rule is defined as the derivative of a variable raised to a numerical exponent. This rule, however, is only limited to variables with numerical exponents. Thus, variables or functions raised to another variable or function cannot use this rule. The power rule can be used to derive any variable raised to exponents such as and limited to:

✔️ Raised to a positive numerical exponent:

$latex y = x^n$
where $latex x$ is a variable and $latex n$ is the positive numerical exponent

✔️ Raised to a negative exponent (rational function in exponential form):

$latex y = \frac{1}{x^n}$
$latex y = x^{-n}$
where $latex x$ is a variable and $latex n$ is the negative numerical exponent

 ✔️ Raised to a rational exponent (radical function in exponential form):

$latex y = \sqrt[n_2]{x^{n_1}}$
$latex y = x^{\frac{n_1}{n_2}}$
where $latex x$ is a variable and $latex \frac{n_1}{n_2} = n$ or the rational numerical exponent $latex n$

And the power rule cannot be used to derive:

❌ Raised to a variable exponent:

$latex y = x^x$

  ❌ Raised to any type of function:

$latex y = x^{f(x)}$

But how exactly do we derive these given functions using the power rule?

The power rule can be written as follows:

$latex f'(x^n) = nx^{n-1}$

where

$latex x$ is the variable
$latex n$ is the value of the numerical exponent of variable $latex x$

In polynomial functions, the power rule is also used by each term, and altogether supported by the sum/difference of derivatives.

In special cases of transcendental functions raised to a numerical exponent, the power rule is supported by the chain rule formula, by using the power rule as the derivative of the outside function f of the composite function $latex f(g(x))$.

We should not take this formula superficially if we aim to deeply understand how a variable raised to a numerical exponent is derived. In order to learn and understand the concepts behind the development of this power rule formula, we need to be familiarized with any proof which would satisfy the statement of the power rule.

---

Proof of The Power Rule Using The Binomial Theorem

To better understand the proof of the power rule using the binomial theorem, you are highly recommended to be familiarized with the topics, The Binomial Theorem, The Slope of a Tangent Line, and Derivatives Using Limits.

We can recall that

$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} \left( {\frac{f(x+h)-f(x)}{h}} \right)$$

By applying limits, we can derive a function f(x). But how about if $latex f(x) = x^n$? If that is the case, we have

$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{(x+h)^n – x^n}{h}} \right)$$

We can evaluate $latex (x+h)^n$ by applying the binomial theorem. Before we apply it to our limit, we can recall that the binomial theorem is an algebraic method of expanding a binomial expression.

The binomial theorem illustrates that in order to expand a quantity of a binomial raised to a numerical exponent, we have

$$(a+b)^n = \displaystyle \sum_{k=0}^{n} {n \choose k} a^{n-k} b^k$$

where

• $latex a$ and $latex b$ can be either a variable or a constant
• $latex n$ is the exponent of the binomial
• $latex k$ is the order of power of the polynomial in the summation.
• $latex {n \choose k}= \frac{n!}{k!(n-k)!}$ ; also called $latex n$ choose $latex k$ combination or $latex {}_n C_k$

By expounding the summation, we have

$$(a+b)^n = {n \choose 0} a^{n-0} \hspace{1.15 pt} b^0 + {n \choose 1} a^{n-1} b^{1}+ …… + {n \choose n-1} a^{n-(n-1)} b^{n-1} + {n \choose n} a^{n-n} b^{n}$$

$$(a+b)^n = \left(\frac{n!}{0! (n-0)!} \right) \cdot a^n + \left(\frac{n!}{1! (n-1)!} \right) \cdot a^{n-1} b+ …… + \left(\frac{n!}{(n-1)! (n-(n-1))!} \right) \cdot a^1 b^{n-1}+ \left(\frac{n!}{n! (n-n)!} \right) \cdot a^0 b^{n}$$

$$(a+b)^n = a^n + na^{n-1} b + …… + nab^{n-1} + b^{n}$$

By applying the binomial theorem on $latex (x+h)^n$, we have

$$(x+h)^n = x^n + nx^{n-1} h + …… + nxh^{n-1} + h^n$$

Substituting this into our limit equation, we have

$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{x^n + nx^{n-1} h + …… + nxh^{n-1} + h^n – x^n}{h}} \right)$$

Simplifying the numerator a little bit since there are similar terms that can be subtracted, we have

$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{nx^{n-1} h + …… + nxh^{n-1} + h^n}{h}} \right)$$

But how can we eliminate the denominator $latex h$ to avoid an undefined result? Notice that all terms in the numerator are multiplied by at least $latex h$ and their least common denominator is $latex h$. Therefore, we can evaluate each term further by dividing them by $latex h$:

$$ \frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( { \left(\frac{nx^{n-1} h}{h} \right)+ …… + \left( \frac{nxh^{n-1} + h^n}{h} \right) } \right)$$

$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( nx^{n-1} h^{1-1}+ …… + nxh^{(n-1)-1} + h^{n-1} \right)$$

$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( nx^{n-1}+ …… + nxh^{n} + h^{n-1} \right)$$

By evaluating our limits through the substitution method, we have

$$\frac{d}{dx} (x^n) = nx^{n-1}+ …… + nx(0)^{n} + (0)^{n-1} $$

We know that zero raised to any exponent except 0 and $latex \infty$ is equal to zero, hence we have

$latex f'(x^n) = nx^{n-1}$

which is now The Power Rule Formula.

---

Proof of The Power Rule Using Logarithmic Differentiation

This is actually the shortest method of proving the power rule formula. However, to better understand the proof of the power rule using logarithmic differentiation, you are highly recommended to be familiarized with the topic, The Logarithmic Differentiation, as a pre-requisite.

We can recall that logarithmic differentiation consists in evaluating both sides of the equation into a logarithm. This is, most of the time, used together with implicit differentiation.

For instance, we are given an equation:

$latex y = x^n$

which if derived is

$latex y’ = f'(x^n)$

But how can we derive this assuming we do not know the power rule formula yet?

By evaluating $latex y = x^n$ logarithmically in order to eliminate the exponent $latex n$, we have

$latex \ln{(y)} = \ln{(x^n)}$

Applying logarithmic properties, we have

$latex \ln{(y)} = n \ln{(x)}$

To differentiate, we can use logarithmic differentiation on both sides of the equation:

$latex \frac{d}{dx} (\ln{(y)}) = \frac{d}{dx} (n \ln{(x)})$

Since the exponent $latex n$ must be only limited to real numbers, then we will treat $latex n$ as a coefficient. Hence, we have

$latex \frac{d}{dx} (\ln{(y)}) = n \frac{d}{dx} (\ln{(x)})$

Then, by applying logarithmic differentiation, we have:

$latex \frac{y’}{y} = \frac{n}{x}$

Equating the equation in terms of $latex y’$ or $latex f'(x^n)$, we have

$latex f'(x^n) = \frac{ny}{x}$

We know that from the beginning of the problem, $latex y = x^n$. Therefore, substitute $latex y$ into the derived equation:

$latex f'(x^n) = \frac{n(x^n)}{x}$

Applying the laws of exponents, we have

$latex f'(x^n) = nx^n \cdot x^{-1}$

$latex f'(x^n) = nx^{n-1}$

which is now The Power Rule Formula.

---

See also

Interested in learning more about the power rule? Take a look at these pages:

• Power Rule – Formula, Proof and Examples
• Power Rule – Examples and Practice Problems