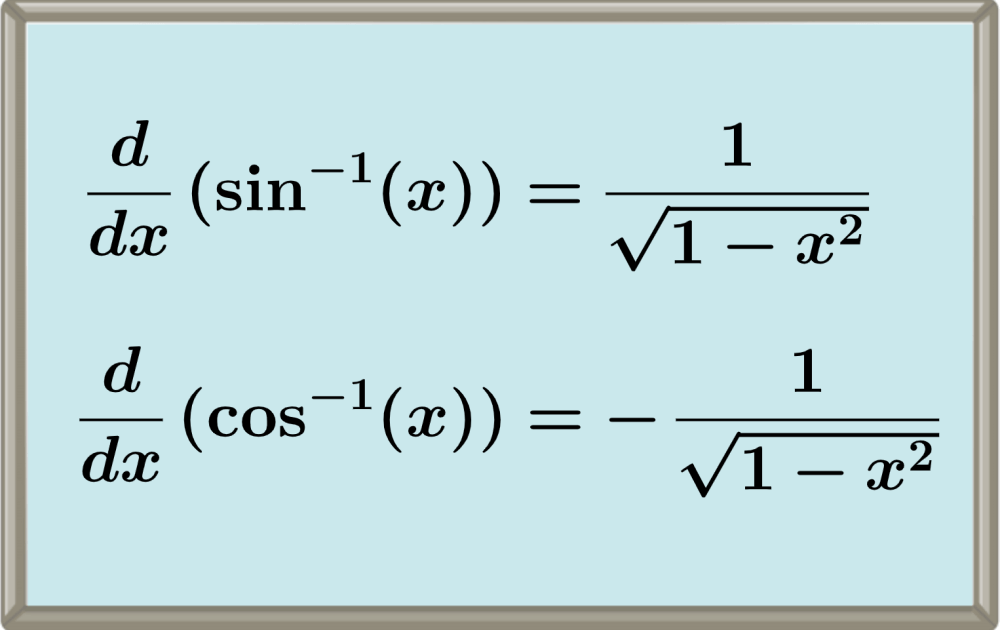Inverse trigonometric functions are functions that “reverse” the effect caused by the original trigonometric function. The derivatives of these functions are obtained using a modified right triangle and the Pythagorean theorem.
Here, we will learn the formulas for the derivatives of the inverse trigonometric functions. Then, we will apply these formulas to solve some exercises.
Formulas for the derivatives of inverse trigonometric functions
Derivative of the inverse sine function (arcsin)
The derivative of the standard inverse sine function is:
$$\frac{d}{dx}(\sin^{-1}(x))=\frac{1}{\sqrt{1-x^2}}$$
You can explore the proof and alternative versions of the inverse sine derivative in this article.
Derivative of the inverse cosine function (arccos)
The derivative of the standard inverse cosine function is:
$$\frac{d}{dx}(\cos^{-1}(x))=-\frac{1}{\sqrt{1-x^2}}$$
You can explore the proof and alternative versions of the inverse cosine derivative in this article.
Derivative of the inverse tangent function (arctan)
The derivative of the standard inverse tangent function is:
$$\frac{d}{dx}(\tan^{-1}(x))=\frac{1}{1+x^2}$$
You can explore the proof and alternative versions of the inverse tangent derivative in this article.
Derivative of inverse cosecant function (arccsc)
The derivative of the standard inverse cosecant function is:
$$\frac{d}{dx}(\csc^{-1}(x))=-\frac{1}{|x|\sqrt{x^2-1}}$$
You can explore the proof and alternative versions of the inverse cosecant derivative in this article.
Derivative of the inverse secant function (arcsec)
The derivative of the standard inverse secant function is:
$$\frac{d}{dx}(\sec^{-1}(x))=\frac{1}{|x|\sqrt{x^2-1}}$$
You can explore the proof and alternative versions of the inverse secant derivative in this article.
Derivative of the inverse cotangent function (arccot)
The derivative of the standard inverse cotangent function is:
$$\frac{d}{dx}(\cot^{-1}(x))=-\frac{1}{1+x^2}$$
You can explore the proof and alternative versions of the inverse cotangent derivative in this article.
Derivatives of inverse trigonometric functions – Examples with answers
EXAMPLE 1
Find the derivative of the following function:
$latex f(x)=\cos^{-1}(5x^2+10)$
Solution
To derive this function, we use the chain rule with $latex y=\cos^{-1}(u)$ and with $latex u=5x^2+10$.
Then, with the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-u^2}}(10x)$$
Substituting $latex u=5x^2+1$, we have:
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-(5x^2+10)^2}}(10x)$$
$$\frac{dy}{dx}=-\frac{10x}{\sqrt{1-(5x^2+10)^2}}$$
EXAMPLE 2
Derive the following function:
$latex f(x)=\sin^{-1}(4x^2+8)$
Solution
This is a composite inverse sine function. Therefore, we use the chain rule with $latex y=\sin^{-1}(u)$ and with $latex u=4x^2+8$.
By the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{\sqrt{1-u^2}}(8x)$$
Substituting $latex u=4x^2+8$, we have:
$$\frac{dy}{dx}=\frac{1}{\sqrt{1-(4x^2+8)^2}}(8x)$$
$$\frac{dy}{dx}=\frac{8x}{\sqrt{1-(4x^2+8)^2}}$$
EXAMPLE 3
Find the derivative of the following function:
$latex f(x)=\tan^{-1}(2x^3+2)$
Solution
In this case, we use the chain rule with $latex y=\tan^{-1}(u)$ and with $latex u=2x^3+2$.
By the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{ 1+u^2}(6x^2)$$
Substituting $latex u=2x^3+2$, we have:
$$\frac{dy}{dx}=\frac{1}{1+(2x^3+2)^2}(6x^2)$$
$$\frac{dy}{dx}=\frac{6x^2}{1+(2x^3+2)^2}$$
EXAMPLE 4
Find the derivative of the following function:
$latex f(x)=\sec^{-1}(8x^2+4)$
Solution
Let’s use the chain rule with $latex y=\sec^{-1}(u)$ and with $latex u=8x^2+4$.
Then, we have:
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{ |u|\sqrt{u^2-1}}(16x)$$
Substituting $latex u=8x^2+4$, we have:
$$\frac{dy}{dx}=\frac{1}{ |8x^2+4|\sqrt{(8x^2+4)^2-1}}(16x)$$
$$\frac{dy}{dx}=\frac{16x}{ 4(2x^2+1)\sqrt{(8x^2+4)^2-1}}$$
$$\frac{dy}{dx}=\frac{4x}{ (2x^2+1)\sqrt{(8x^2+4)^2-1}}$$
Derivatives of inverse trigonometric functions – Practice problems


See also
Interested in learning more about derivatives? You can look at these pages: