The derivative of the inverse cotangent function is equal to -1/(1+x2). This derivative can be proved using the Pythagorean theorem and Algebra.
In this article, we will learn how to derive the inverse cotangent function. We will see general considerations with its notation, a proof, the graphical comparison of the function and its derivative, and some examples.
CALCULUS
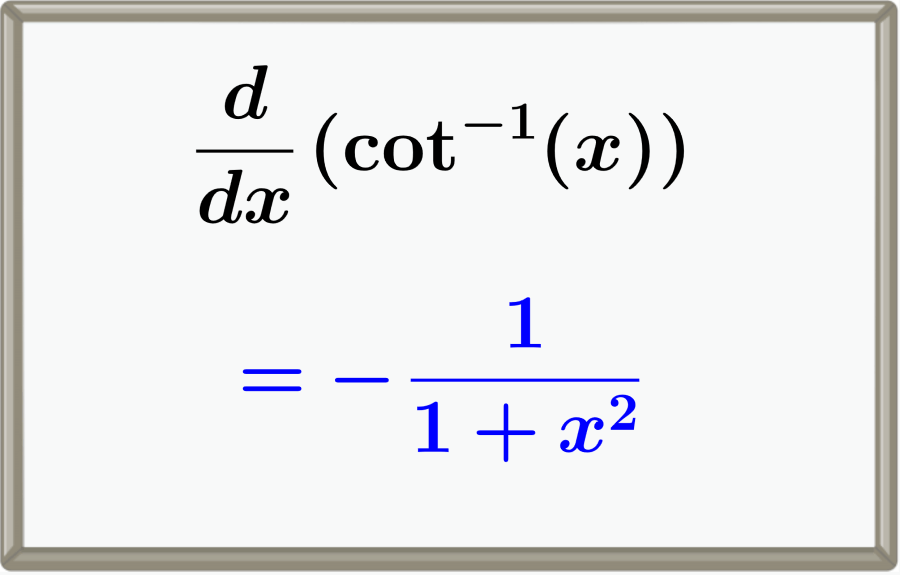
Relevant for…
Learning about the proof and graphs of the derivative of arccot of x.
CALCULUS
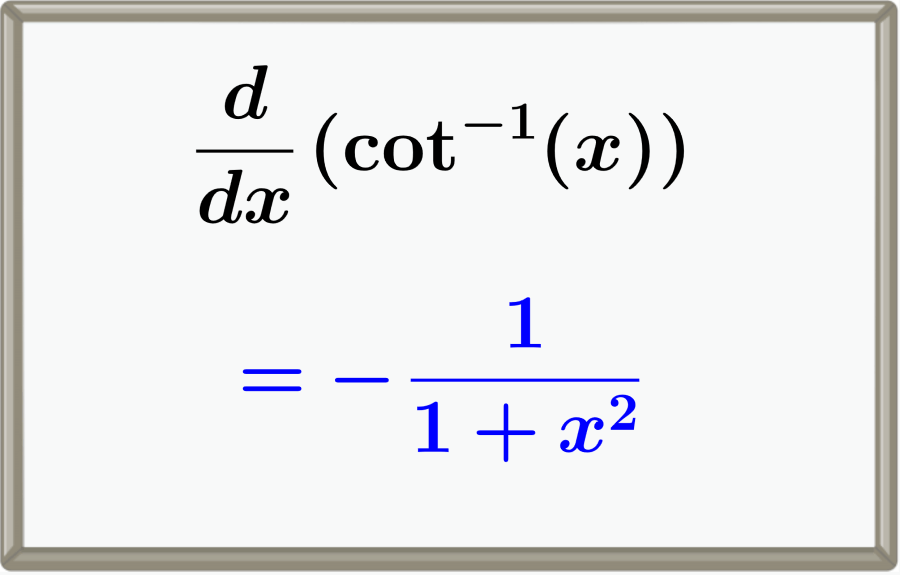
Relevant for…
Learning about the proof and graphs of the derivative of arccot of x.
Avoid confusion in using the denotations arccot(x), cot-1(x),
1
/
cot(x) , and cotn(x)
Let’s start by clarifying the use of the different denotations between $latex \text{arccot}(x)$, $latex \cot^{-1}{(x)}$, $latex \frac{1}{\cot {(x)}}$ and $latex \cot^{n}{(x)}$, since interchanging these symbols, we can get derivation errors.
Summarizing the definition of these symbols, we have
$latex \text{arccot}(x) = \cot^{-1}{(x)}$
The symbols $latex \text{arccot}$ and $latex \cot^{-1}$ are used to denote the inverse cotangent. \text{arccot} is used as the verbal symbol of the inverse cotangent function, while $latex \cot^{-1}$ is used as the mathematical symbol of the inverse cotangent function for a more formal function.
In the case of the denotation $latex \cot^{-1}{(x)}$, we must consider that $latex -1$ is not an algebraic exponent of a cotangent. The $latex -1$ used for the inverse cotangent represents that the cotangent is inverse and not raised to $latex -1$.
Therefore,
$latex \cot^{-1}{(x)} \neq \frac{1}{\cot{(x)}}$
And givens such as $latex \cot^{2}{(x)}$ or $latex \cot^{n}{(x)}$, where n is any algebraic exponent of a non-inverse cotangent, MUST NOT use the inverse cotangent formula since in these givens, both the 2 and any exponent n are treated as algebraic exponents of a non-inverse cotangent.
Proof of the Derivative of the Inverse Cotangent Function
In this proof, we will mainly use the concepts of a right triangle, the Pythagorean theorem, the trigonometric functions of cotangent and cosecant, and some basic algebra. Just like in the previous figure as a reference sample for a given right triangle, suppose we have that same triangle $latex \Delta ABC$, but this time, let’s change the variables for an easier illustration.
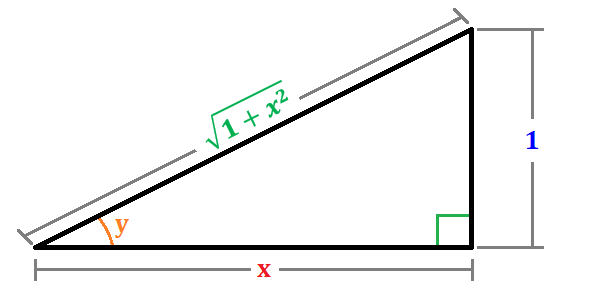
where for every one-unit of a side opposite to angle y, there is a side x adjacent to angle y and a hypotenuse equal to $latex \sqrt{1+x^2}$.
Using these components of a right-triangle, we can find the angle y by using Cho-Sha-Cao, particularly the cotangent function by using its adjacent and opposite sides.
$latex \cot{(\theta)} = \frac{adj}{opp}$
$latex \cot{(y)} = \frac{x}{1}$
$latex \cot{(y)} = x$
Now, we can implicitly derive this equation by using the derivative of trigonometric function of cotangent for the left-hand side and power rule for the right-hand side. Doing so, we have
$latex \frac{d}{dx} (\cot{(y)}) = \frac{d}{dx} (x)$
$latex \frac{d}{dx} (\cot{(y)}) = 1$
$latex \frac{dy}{dx} (-\csc^{2}{(y)}) = 1$
$latex \frac{dy}{dx} = \frac{1}{-\csc^{2}{(y)}}$
$latex \frac{dy}{dx} = -\frac{1}{\csc^{2}{(y)}}$
Getting the cosecant of angle y from our given right-triangle, we have
$latex \csc{(y)} = \frac{hyp}{opp}$
$latex \csc{(y)} = \frac{\sqrt{1+x^2}}{1}$
Since we need to substitute $latex \csc{(y)}$ into $latex \csc^{2}{(y)}$, we need to square both sides
$latex \csc^{2}{(y)} = \left(\frac{\sqrt{1+x^2}}{1}\right)^2$
$latex \csc^{2}{(y)} = \left(\sqrt{1+x^2}\right)^2$
$latex \csc^{2}{(y)} = 1+x^2$
We can then substitute $latex \csc^{2}{(y)}$ to the implicit differentiation of $latex \cot{(y)} = x$
$latex \frac{dy}{dx} = -\frac{1}{\csc^{2}{(y)}}$
$latex \frac{dy}{dx} = -\frac{1}{1+x^2}$
Therefore, algebraically solving for the angle y and getting its derivative, we have
$latex \cot{(y)} = x$
$latex y = \frac{x}{\cot}$
$latex y = \cot^{-1}{(x)}$
$latex \frac{dy}{dx} = \frac{d}{dx} \left( \cot^{-1}{(x)} \right)$
$latex \frac{dy}{dx} = -\frac{1}{1+x^2}$
which is now the derivative formula for the inverse cotangent of x.
Now, for the derivative of an inverse cotangent of any function other than x, we may apply the derivative formula of inverse cotangent together with the chain rule formula. By doing so, we have
$latex \frac{dy}{dx} = \frac{d}{du} \cot^{-1}{(u)} \cdot \frac{d}{dx} (u)$
$latex \frac{dy}{dx} = -\frac{1}{1+u^2} \cdot \frac{d}{dx} (u)$
where $latex u$ is any function other than x.
Graph of Inverse Cotangent x VS. The Derivative of Inverse Cotangent x
Given the function
$latex f(x) = \cot^{-1}{(x)}$
its graph is
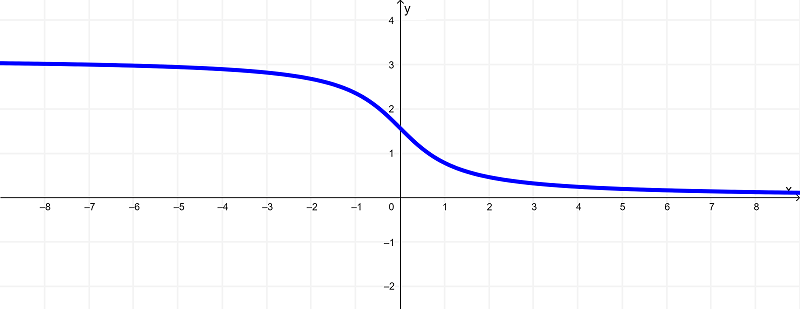
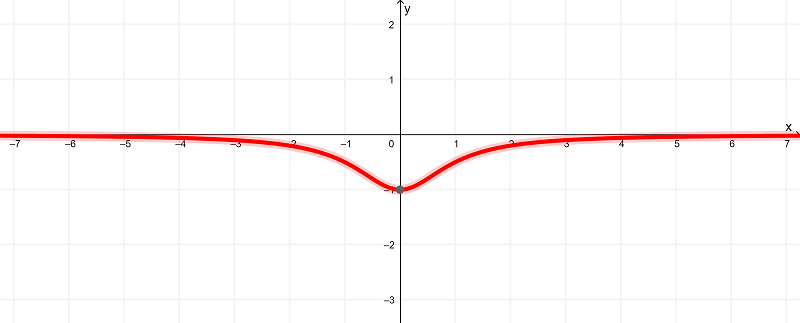
And as we know by now, by deriving $latex f(x) = \cot^{-1}{(x)}$, we get
$latex f'(x) = -\frac{1}{1+x^2}$
which is illustrated graphically as
Illustrating both graphs in one, we have
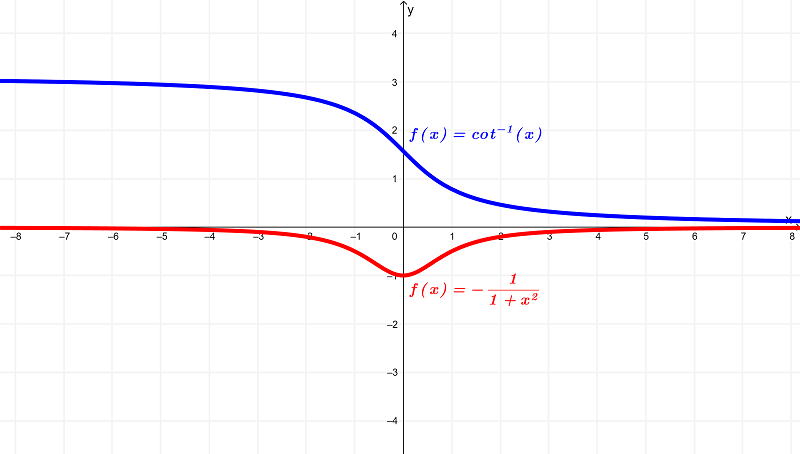
Analyzing the differences of these functions through these graphs, you can observe that the original function $latex f(x) = \cot^{-1}{(x)}$ has a domain of
$latex (-\infty,\infty)$ or all real numbers
and exists within the range of
$latex (0,\pi)$ or $latex 0<y<\pi$
whereas the derivative $latex f'(x) = -\frac{1}{1+x^2}$ has a domain of
$latex (-\infty,\infty)$ or all real numbers
and exists within the range of
$latex [-1, 0)$ or $latex -1 \leq y < 0$
Examples
Here are some examples of how to derive a composite inverse cotangent function.
EXAMPLE 1
What is the derivative of $latex f(x) = \cot^{-1}(11x)$?
Solution
We have a composite inverse cotangent function, so let’s use the chain rule to derive it.
Considering $latex u=11x$ as the inner function, we can write $latex f(u)=\tan^{-1}(u)$. Therefore, applying the chain rule, we have:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\frac{1}{1+u^2} \times 11$$
Substituting $latex u=11x$ back into the function, we have:
$$\frac{dy}{dx}=-\frac{11}{1+(11x)^2}$$
$$\frac{dy}{dx}=-\frac{11}{1+121x^2}$$
EXAMPLE 2
Find the derivative of the function $latex F(x) = \cot^{-1}(x^3+5)$
Solution
We are going to use the chain rule. Therefore, we write the inverse tangent function as $latex f (u) = \cot^{-1}(u)$, where $latex u = x^3+5$.
Now, we calculate the derivative of the outer function $latex f(u)$:
$$\frac{d}{du} ( \cot^{-1}(u) ) = -\frac{1}{1+u^2}$$
Then, we calculate the derivative of the inner function $latex g(x)=u=x^3+5$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(x^3+5)$$
$$\frac{d}{dx}(g(x)) = 3x^2$$
The chain rule tells us that we have to multiply the derivative of the outer function by the derivative of the inner function:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -\frac{1}{1+u^2} \cdot 3x^2$$
Finally, we substitute $latex u$ back in and simplify:
$$\frac{dy}{dx} = -\frac{1}{1+(x^3+5)^2} \cdot 3x^2$$
$$\frac{dy}{dx} = -\frac{3x^2}{1+x^6+10x^3+25}$$
$$F'(x) = -\frac{3x^2}{x^6+10x^3+26}$$
EXAMPLE 3
If we have the function $latex f(x) = \cot^{-1}(\sqrt{x})$, what is its derivative?
Solution
The square root function is the inner function. Therefore, since $latex u=\sqrt{x}$ is equal to $latex u=x^{\frac{1}{2}}$, we have the following derivative:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Since we have $latex f(u)=\cot^{-1}(u)$ applying the chain rule gives us:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\frac{1}{1+u^2} \times \frac{1}{2}x^{-\frac{1}{2}}$$
Substituting $latex u=\sqrt{x}$ and simplifying, we have:
$$\frac{dy}{dx}=-\frac{1}{1+(\sqrt{x})^2} \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{1+x} \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x}(1+x)}$$
Practice of derivatives of composite inverse cotangent functions
See also
Interested in learning more about the derivatives of trigonometric functions? Take a look at these pages:
- Derivative of arcsin (Inverse Sine) With Proof and Graphs
- Derivative of arccos (Inverse Cosine) With Proof and Graphs
- Derivative of arctan (Inverse Tangent) With Proof and Graphs
- Derivative of arcsec (Inverse Secant) With Proof and Graphs
- Derivative of arccsc (Inverse Cosecant) With Proof and Graphs
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
