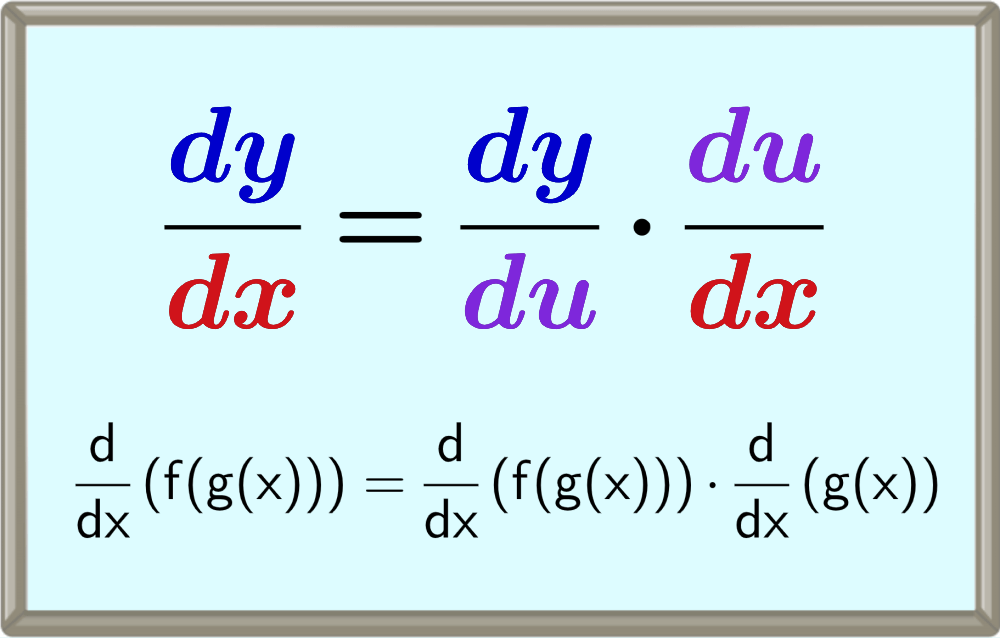Chain Rule of Derivatives – Examples with Answers

The first thing we need to do is to write the chain rule formula for our reference:

$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{x}(g(x))$$

Assuming you are a beginner, let’s identify the functions involved from function composition:

We have

$latex H(x) = (x+2)^2$

If we use the substitution $latex u = g(x) = x+2$, we can write

$latex f(g(x)) = f(u)$

$latex f(u) = u^2$

Applying the chain rule formula, we have:

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{x}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^2) \cdot \frac{d}{x}(x+2)$$

$$\frac{d}{dx} (H(x)) = (2u) \cdot (1)$$

Since $latex u = x+2$, let us substitute back:

$$\frac{d}{dx} (H(x)) = [2 \cdot (x+2)] \cdot (1)$$

Simplifying algebraically, we have

$latex H'(x) = 2(x+2)$

And the final answer is:

$latex H'(x) = 2x + 4$

If we use the substitution $latex g(x) = u=x^3 – 3x^2 + 2x$, we have:

$latex f(g(x)) = f(u)$

$latex f(u) = u^5$

Applying the chain rule formula, we have:

$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^5) \cdot \frac{d}{dx}(x^3 – 3x^2 + 2x)$$

$$\frac{d}{dx} (H(x)) = (5u^4) \cdot (3x^2-6x+2)$$

Now, we can substitute $latex u=x^3 – 3x^2 + 2x$ back in:

$$\frac{d}{dx} (H(x)) = [5 \cdot (x^3 – 3x^2 + 2x)^4]\cdot (3x^2-6x+2)$$

Simplifying algebraically, we have

$$H'(x) = (5x^3-15x^2+10x)^4 \cdot (3x^2-6x+2)$$

And the final answer is:

$$H'(x) = (5x^3-15x^2+10x)^4 (3x^2-6x+2)$$

If we consider $latex g(x)=u=3x^2-1$, we can write as follows:

$latex f(g(x)) = f(u)$

$latex f(u) = \ln{(u)}$

Then, we apply the chain rule:

$$ \frac{d}{dx} (F(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{x}(g(x))$$

$$\frac{d}{dx} (F(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{x}(g(x))$$

$$\frac{d}{dx} (F(x)) = \frac{d}{du} (\ln(u)) \cdot \frac{d}{x}(3x^2-1)$$

$$\frac{d}{dx} (F(x)) = (\frac{1}{u}) \cdot (6x)$$

Substituting $latex u=3x^2-1$ back in, we have:

$$\frac{d}{dx} (F(x)) = (\frac{1}{3x^2-1}) \cdot (6x)$$

Simplifying, we have

$$F'(x) = \frac{6x}{3x^2-1}$$

And the final answer is:

$$F'(x) = \frac{6x}{3x^2-1}$$

We start by considering that the inner function is $latex g(x)=u=3x^2+1$. Then, the composition of functions can be written as:

$latex f(g(x)) = f(u)$

$latex f(u) = e^u$

Applying the chain rule formula, we have:

$$\frac{d}{dx} (G(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{x}(g(x))$$

$$\frac{d}{dx} (G(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{x}(g(x))$$

$$\frac{d}{dx} (G(x)) = \frac{d}{du} (e^u) \cdot \frac{d}{x}(3x^2+1)$$

$$\frac{d}{dx} (G(x)) = (e^u) \cdot (6x)$$

Since $latex u = 3x^2+1$, we substitute in the derivative:

$$\frac{d}{dx} (G(x)) = (e^{3x^2+1}) \cdot (6x)$$

$$G'(x) = 6x \cdot e^{3x^2+1}$$

And the final answer is:

$$G'(x) = 6xe^{3x^2+1}$$

If we consider the inner function as $latex g(x) = u=x^3-9$, then

$latex f(g(x)) = f(u)$

$latex f(u) = \cos(u)$

Applying the chain rule formula, we have:

$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (\cos(u)) \cdot \frac{d}{dx}(x^3 – 9)$$

$$\frac{d}{dx} (H(x)) = (-\sin(u)) \cdot (3x^2)$$

Since $latex u = g(x)$, we substitute $latex g(x)$ into $latex u$:

$$\frac{d}{dx} (H(x)) = (-\sin(x^3-9)) \cdot (3x^2)$$

Simplifying, we have

$latex H'(x) = -3x^2 \cdot \sin{(x^3-9)}$

And the final answer is:

$latex H'(x) = -3x^2 \sin{(x^3-9)}$

Let us identify the functions involved from the composition of functions:

We have

$$H(x) = \sqrt[3]{x^3 – 3x^2 + 2x}$$

Since this is a radical function, it is always recommended to rewrite it from radical to exponent form to make it derivable. Rewriting, we have

$$ H(x) = (x^3 – 3x^2 + 2x)^{\frac{1}{3}}$$

If $latex g(x) = u=x^3-3x^2+2x$, then

$latex f(g(x)) = f(u)$

$latex f(u) = u^{\frac{1}{3}}$

By using the chain rule with these functions, we have:

$$ \frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$

$$ \frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^{\frac{1}{3}} ) \cdot \frac{d}{dx}(x^3 – 3x^2 + 2x)$$

$$\frac{d}{dx} (H(x)) = (\frac{1}{3} u^{-\frac{2}{3}}) \cdot (3x^2-6x+2)$$

Now, we can substitute $latex u=g(x)$ back in:

$$\frac{d}{dx} (H(x)) = [(\frac{1}{3} \cdot (x^3 – 3x^2 + 2x)^{-\frac{2}{3}})]\cdot (3x^2-6x+2)$$

Simplifying, we have

$$H'(x) = \frac{1}{3 \cdot (x^3 – 3x^2 + 2x)^{\frac{2}{3}}} \cdot (3x^2-6x+2)$$

$$H'(x) = \frac{3x^2-6x+2}{3 \cdot (x^3 – 3x^2 + 2x)^{\frac{2}{3}}}$$

And the final answer is:

$$H'(x) = \frac{3x^2-6x+2}{3 \sqrt[3]{(x^3 – 3x^2 + 2x)^2}}$$
en forma radical

Considering $latex g(x) = u=\sec(x)$ as the inner function, we can write

$latex f(g(x)) = f(u)$

$latex f(u) = u^5$

Using the chain rule, we have:

$$\frac{d}{dx} (H(x)) = \frac{d}{dx} (f(g(x)) ) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^5 ) \cdot \frac{d}{dx}(\sec{(x)})$$

$$\frac{d}{dx} (H(x)) = (5u^4) \cdot (\sec{(x)} \tan{(x)})$$

Now, we can substitute $latex u=\sec(x)$ back into the derivative:

$$\frac{d}{dx} (H(x)) = [5(\sec(x))^4] \cdot (\sec(x) \tan(x))$$

Simplifying, we have

$$H'(x) = 5 \cdot \sec{(x)} \cdot \sec^{4}{(x)} \cdot \tan(x)$$

$$H'(x) = 5 \cdot \tan(x) \cdot \sec^{5}{(x)}$$

And the final answer is:

$latex H'(x) = 5 \tan{(x)} \sec^{5}{(x)}$

If $latex g(x) = u=x^3+e^x$, then

$latex f(g(x)) = f(u)$

$latex f(u) = \log_{7}{u}$

Applying the chain rule formula, we have:

$$\frac{d}{dx} (F(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (F(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (F(x)) = \frac{d}{du} (\log_{7}{u} ) \cdot \frac{d}{dx}(x^3+e^x)$$

$$\frac{d}{dx} (F(x)) = \left(\frac{1}{u \ln(7)} \right) \cdot (3x^2+e^x)$$

Now, let’s substitute $latex u=x^3+e^x$:

$$\frac{d}{dx} (F(x)) = \left(\frac{1}{(x^3+e^x) \ln(7)} \right) \cdot (3x^2+e^x)$$

Simplifying algebraically, we have

$$\frac{d}{dx} (F(x)) = \left(\frac{1}{(x^3+e^x) \ln{(7)}} \right) \cdot (3x^2+e^x)$$

$$\frac{d}{dx} (F(x)) = \left(\frac{3x^2+e^x}{(x^3+e^x) \ln{(7)}} \right)$$

And the final answer is:

$$F'(x) = \left(\frac{3x^2+e^x}{(x^3+e^x) \ln{(7)}} \right)$$

Considering $latex g(x)=u=\frac{x-1}{x+2}$ as the inner function, we have:

$latex f(g(x)) = f(u)$

$latex f(u) = \cot^{-1}{(u)}$

Now, we can use the chain rule with the functions we have defined:

$$\frac{d}{dx} (F(x)) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{dx}(g(x))$$

$$ \frac{d}{dx} (F(x)) = \frac{d}{du} (f(u)) \cdot \frac{d}{dx}(g(x))$$

$$\frac{d}{dx} (F(x)) = \frac{d}{du} (\cot^{-1}(u)) \cdot \frac{d}{dx} \left(\frac{x-1}{x+2} \right)$$

$$\frac{d}{dx} (F(x)) = \left(-\frac{1}{u^2+1} \right) \cdot \left(\frac{2}{(x+1)^2} \right)$$

Since $latex u = g(x)$, we substitute $latex g(x)$ into $latex u$:

$$\frac{d}{dx} (F(x)) = \left(-\frac{1}{ \left(\frac{x-1}{x+1} \right)^2+1} \right) \cdot \left(\frac{2}{(x+1)^2} \right)$$

Simplifying, we have

$$\frac{d}{dx} (F(x)) = -\frac{2}{\left(\left(\frac{x-1}{x+1} \right)^2+1\right) \cdot (x+1)^2}$$

$$\frac{d}{dx} (F(x)) = -\frac{1}{x^2+1}$$

And the final answer is:

$$F'(x) = -\frac{1}{x^2+1}$$

This is a more complex case since the function $latex H(x)$ is a composition of four functions.

If $latex f(g(h(j(x)))) = u$, then

$latex f(g(h(j(x)))) = f(u)$
$latex f(u) = u^2$

If $latex g(h(j(x))) = v$, then

$latex g(h(j(x))) = g(v)$
$latex g(v) = \tan{(v)}$

If $latex h(j(x)) = w$, then

$latex h(j(x)) = h(w)$
$latex h(w) = e^w$

$latex w = j(x) = 3x$

If $latex f(g(h(j(x)))) = f(u)$, then

$$\frac{d}{dx} [f(g(h(j(x))))] = \frac{d}{du} [f(u)]$$

If $latex g(h(j(x))) = g(v)$, then

$$\frac{d}{dx} [g(h(j(x)))] = \frac{d}{dv} [g(v)]$$

If $latex h(j(x)) = h(w)$, then

$$\frac{d}{dx} [h(j(x))] = \frac{d}{dw} [h(w)]$$

Adjusting our chain rule formula for the derivative of compositions of four functions, we have

$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(h(j(x)))) \right)\cdot \frac{d}{dx} \left(g(h(j(x))) \right) \cdot \left(h(j(x)) \right) \cdot \frac{d}{dx}(j(x))$$

$$\frac{d}{dx} (H(x)) = \frac{d}{du} \left(f(u)) \right) \cdot \frac{d}{dv} \left(g(v)) \right) \cdot \frac{d}{dw} \left(h(w)) \right) \cdot \frac{d}{dx}(j(x))$$

Applying our adjusted chain rule formula for the derivative of the composition of four functions, we have

$$\frac{d}{dx} (H(x)) = \frac{d}{du} (u^2) \cdot \frac{d}{dv} (\tan{(v)}) \cdot \frac{d}{dw} (e^w) \cdot \frac{d}{dx}(3x)$$

$$\frac{d}{dx} (H(x)) = (2u) \cdot (\sec^{2}{(v)}) \cdot (e^w) \cdot (3)$$

Since $latex u = g(h(j(x)))$, $latex v = h(j(x))$ and $latex w = j(x)$, let’s apply these substitutions:

$$\frac{d}{dx} (H(x)) = (2(\tan{(e^{3x})})) \cdot (\sec^{2}{(e^{3x})}) \cdot (e^{3x}) \cdot (3)$$

Simplifying algebraically, we have

$$\frac{d}{dx} (H(x)) = 2 \cdot 3 \cdot e^{3x} \cdot \tan{(e^{3x})} \cdot \sec^{2}{(e^{3x})}$$

$$H'(x) = 6 \cdot (e^{3x}) \cdot \tan{(e^{3x})} \cdot \sec^{2}{(e^{3x})}$$

And the final answer is:

$$ H'(x) = 6 \cdot (e^{3x}) \tan{(e^{3x})} \sec^{2}{(e^{3x})}$$

As you can see from our solution to this problem, deriving compositions of four functions, you will realize why the chain rule was coined from the term “chain”.