Arccos Calculator (Inverse Cosine)
cos-1() =
Degrees:
Radians:
π radians:
Graph of inverse cosine
The domain considered is -1 ≤ x ≤ 1.
The range considered is 0 ≤ y ≤ π.
This calculator allows you to determine the inverse cosine of an entered value. The answer will be displayed in degrees, radians, and π radians, only considering the range 0 ≤ y ≤ π.
Below you will find additional information on using the arccos calculator. In addition, you can also learn about the definition of inverse cosine, its graph, and some important values.
How to use the inverse cosine calculator?
Step 1: Enter the value of x in the corresponding input box. The entered value must be in the domain -1 ≤ x ≤ 1.
Step 2: The corresponding angle in degrees will be displayed in the right panel.
Step 3: The boxes at the bottom will show the angle in radians and π radians.
Difference between results in degrees, radians, and π radians
One complete revolution of a circle is equal to 360° or 2π radians. This means that 180° is equal to π radians.
The difference between π radians and radians is simply that the result in “radians” is already multiplied by π, while in “π radians” it is not. For example, the result 1.5 π radians is equal to 4.712, since π has a value of approximately 3.1415…
What is inverse cosine?
The inverse cosine, also called the arc cosine and denoted cos-1(x) or also arccos(x), is the inverse cosine function. This means that the inverse cosine reverses the effects of the cosine function.
For example, the cosine of 60° is equal to 0.5. This means that the inverse cosine of 0.5 is equal to 60°.
Inverse cosine can be used when we want to find an angle, and we have the proportions of the sides of a triangle. For example, we can find angle A in the following triangle using arccos(x), where x equals b/c.
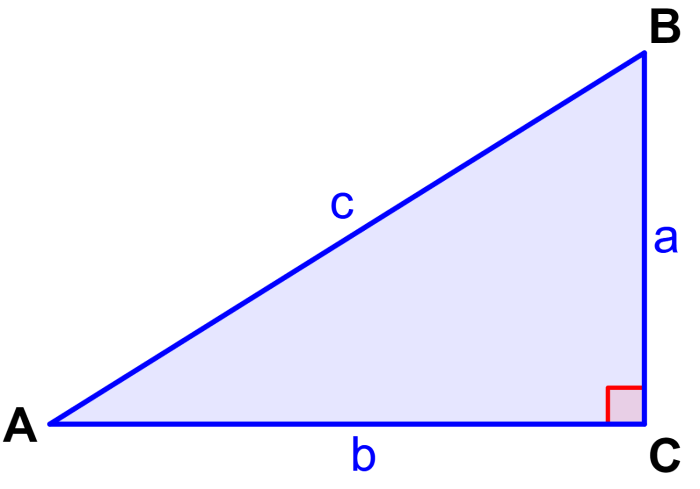
Why does the inverse cosine function only accept values from -1 to 1?
The inverse cosine function has a domain from -1 to 1 because it is the inverse cosine function. This means that the domain and range are swapped.
Considering the cosine function, there is no angle that we can use to get a value greater than 1 or less than -1. Cosine output values are always between -1 and 1, therefore inverse cosine input values must also be between those values.
Graph of inverse cosine
The arc cosine function can be graphed by considering specific intervals for the input and output values. In the inverse cosine used in this calculator, the x values range from -1 to 1 and the output or y values range from 0 to π.
Inverse cosine domain
Using the graph, we can see that the domain of the function, that is, the values of x, range from -1 to 1. Therefore, the domain is -1 ≤ x ≤ 1.
Inverse cosine range
In the graph, we can see that the function has a range from 0 to π. Therefore, its range is 0 ≤ y ≤ π.
Table of inverse cosines of common values
| Value of x | arccos(x)(rad) | arccos(x)(°) |
|---|---|---|
| -1 | π | 180° |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| 0 | π/2 | 90° |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 1 | 0 | 0° |
Related calculators:
- Arcsin Calculator (Inverse Sine) – Degrees and Radians
- Arctan Calculator (Inverse Tangent) – Degrees and Radians
- Arcsec Calculator (Inverse Secant) – Degrees and Radians
- Arccsc Calculator (Inverse Cosecant) – Degrees and Radians
- Arccot Calculator (Inverse Cotangent) – Degrees and Radians
You can explore other calculators here.
