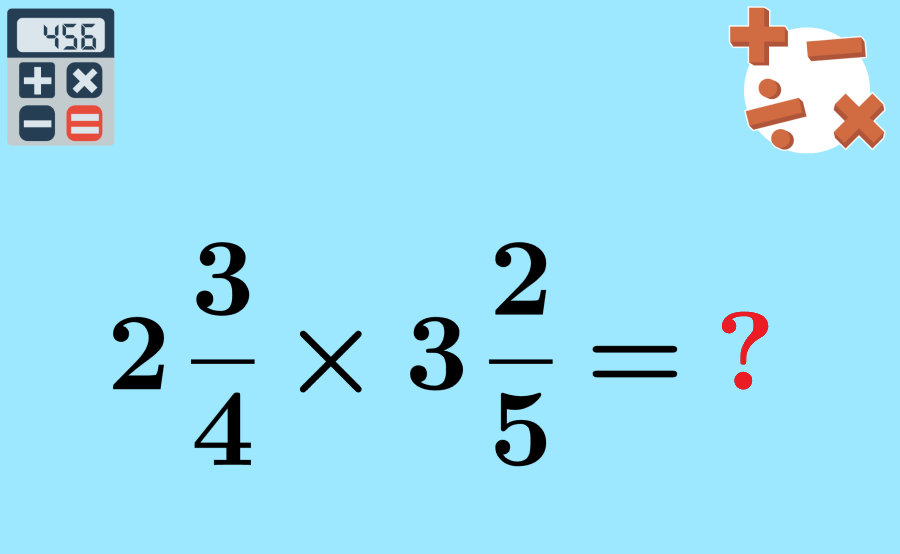To multiply two or more mixed fractions, we have to start by converting the mixed fractions to improper fractions. Then, we simply multiply the numerators and denominators separately. Finally, we simplify the resulting fraction if possible.
Here, we will learn to multiply mixed fractions step by step. In addition, we will solve some practice problems to apply everything learned.
Steps to multiply mixed fractions
Mixed fractions are fractions that are made up of a fractional part and a whole number part. On the other hand, improper fractions only have the fractional part.
Mixed fractions can be converted to improper fractions and vice versa. Therefore, we follow the steps below to multiply mixed fractions:
Step 1: Convert the mixed fractions to improper fractions.
To convert mixed fractions to improper fractions, we multiply the integer part by the denominator and add the result to the numerator.
Step 2: Multiply the numerators.
Step 3: Multiply the denominators.
Step 4: Simplify the resulting fraction if possible.
Multiplying mixed fractions – Examples with answers
The steps used to multiply mixed fractions seen above are used to solve the following examples. Try to solve the problems before looking at the solution.
EXAMPLE 1
Solve the multiplication of fractions $latex 1\frac{1}{2}\times \frac{1}{3}$.
Solution
Step 1: Convert the first mixed fraction to improper fraction:
$$1\frac{1}{2}\times \frac{1}{3}$$
$$=\frac{3}{2}\times \frac{1}{3}$$
Step 2: Multiplying the numerators, we have:
$$=\frac{3\times 1}{2\times 3}$$
$$=\frac{3}{2\times 3}$$
Step 3: Multiplying the denominators, we have:
$$=\frac{3}{6}$$
Step 4: We can simplify by dividing by 3:
$$=\frac{1}{2}$$
EXAMPLE 2
Find the product of the multiplication $latex 2\frac{2}{3}\times 1\frac{1}{5}$.
Solution
Step 1: We convert both mixed fractions to improper fractions:
$$2\frac{2}{3}\times 1\frac{1}{5}$$
$$=\frac{8}{3}\times \frac{6}{5}$$
Step 2: By multiplying the numerators, we have:
$$=\frac{8\times 6}{3\times 5}$$
$$=\frac{48}{3\times 5}$$
Step 3: By multiplying the denominators, we have:
$$=\frac{48}{15}$$
Step 4: We divide by 3 to simplify and then convert to a mixed fraction:
$$=\frac{16}{5}$$
$$=3\frac{1}{5}$$
EXAMPLE 3
Solve the multiplication of fractions $latex 1\frac{4}{5}+3\frac{1}{7}$.
Solution
Step 1: We convert both mixed fractions to improper fractions:
$$1\frac{4}{5}\times 3\frac{1}{7}$$
$$=\frac{9}{5}\times \frac{22}{7}$$
Step 2: Multiplying the numerators, we have:
$$=\frac{9\times 22}{5\times 7}$$
$$=\frac{198}{5\times 7}$$
Step 3: Multiplying the denominators, we have:
$$=\frac{198}{35}$$
Step 4: Converting to a mixed fraction, we have:
$$=5\frac{23}{35}$$
EXAMPLE 4
Solve the multiplication of mixed fractions $latex \frac{1}{4}\times 1\frac{1}{2} \times \frac{1}{3}$.
Solution
Step 1: Convert the mixed fraction to an improper fraction:
$$\frac{1}{4}\times 1\frac{1}{2} \times \frac{1}{3}$$
$$=\frac{1}{4}\times \frac{3}{2} \times \frac{1}{3}$$
Step 2: By multiplying the numerators, we have:
$$=\frac{1\times 3 \times 1}{4\times 2 \times 3}$$
$$=\frac{3}{4\times 2 \times 3}$$
Step 3: By multiplying the denominators, we have:
$$=\frac{3}{24}$$
Step 4: We can simplify by dividing by 3:
$$=\frac{1}{8}$$
EXAMPLE 5
Find the product of the mixed fractions $latex 1\frac{2}{3}\times \frac{3}{4}\times 2\frac{1}{5}$.
Solution
Step 1: We convert both mixed fractions to improper fractions:
$$1\frac{2}{3}\times \frac{3}{4}\times 2\frac{1}{5}$$
$$=\frac{5}{3}\times \frac{3}{4}\times \frac{11}{5}$$
Step 2: Multiplying the numerators, we have:
$$=\frac{5\times 3 \times 11}{3\times 4 \times 5}$$
$$=\frac{165}{3\times 4 \times 5}$$
Step 3: Multiplying the denominators, we have:
$$=\frac{165}{60}$$
Step 4: We simplify by dividing by 15 and converting to a mixed fraction:
$$=\frac{11}{4}$$
$$=2\frac{3}{4}$$
EXAMPLE 6
Solve the multiplication of fractions $latex 2\frac{3}{4} \times 1\frac{2}{3}\times 1\frac{2}{5}$.
Solution
Step 1: We convert the mixed fractions to improper fractions:
$$2\frac{3}{4}\times 1\frac{2}{3}\times 1\frac{2}{5}$$
$$=\frac{11}{4}\times \frac{5}{3}\times \frac{7}{5}$$
Step 2: By multiplying the numerators, we have:
$$=\frac{11\times 5 \times 7}{4\times 3 \times 5}$$
$$=\frac{385}{4\times 3 \times 5}$$
Step 3: By multiplying the denominators, we have:
$$=\frac{385}{60}$$
Step 4: We can simplify by dividing by 5 and converting to a mixed fraction:
$$=\frac{77}{12}$$
$$=6\frac{5}{12}$$
Multiplying mixed fractions – Practice problems
Apply everything you have learned about the multiplication of mixed fractions to solve the following practice problems.
See also
Interested in learning more about multiplying and dividing fractions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
