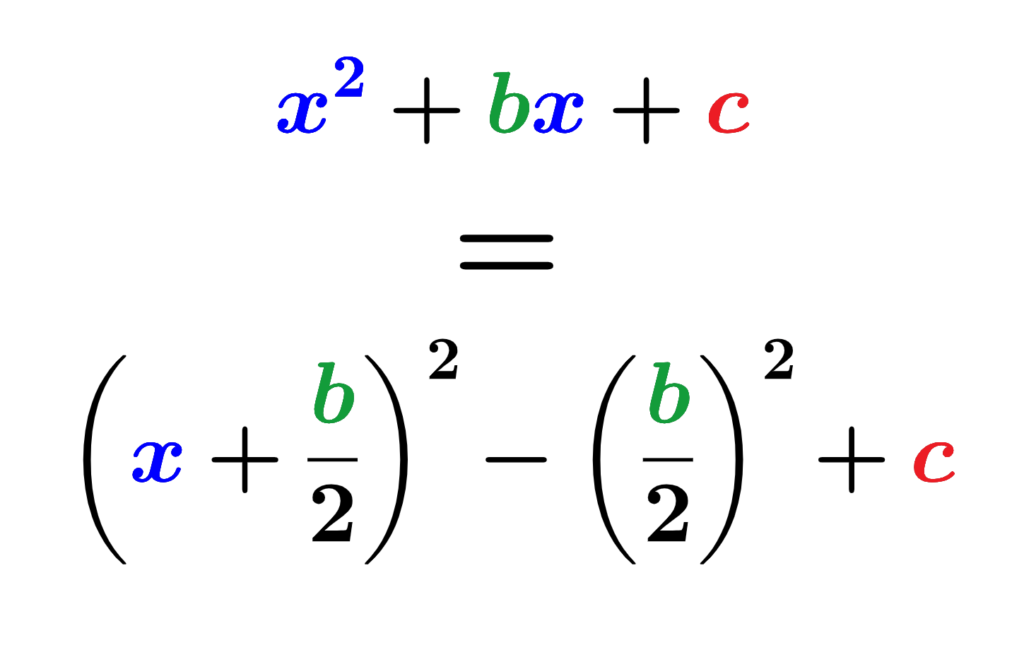To solve quadratic equations using the method of completing the square, we need to convert an equation from the form ax2+bx+c to the form a(x–h)2=k. Then, we can take the square root of both sides. This method can allow us to solve a quadratic equation easily.
In this article, we will learn how to solve quadratic equations by completing the square. We’ll go through a step-by-step process and use it to solve some practice problems.
Solve Quadratic Equations by Completing the Square – Step by Step Method
To solve quadratic equations via the method of completing the square, we can follow the steps below, assuming we start with an equation written in the form $latex ax^2+bx+c=0$.
Step 1: When the coefficient of the quadratic term (a) is different from 1, we divide the quadratic equation by a so that we obtain an equation with a value of a equal to 1:
$latex x^2+bx+c=0$
Step 2: We take the coefficient b and divide it by 2:
$$\left(\frac{b}{2}\right)$$
Step 3: We take the expression from step 2 and square it:
$$\left(\frac{b}{2}\right)^2$$
Step 4: We add and subtract the expression obtained in step 3 to the equation obtained in step 1:
$$x^2+bx+\left(\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Step 5: We apply the identity $latex x^2+2xy+y^2=(x+y)^2$ to factor the quadratic equation:
$$\left(x+\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Step 6: We multiply the expression resulting from step 5 by the number by which we divided in step 1 and simplify it to obtain an equation of the following form:
$latex (x-h)^2+k=0$
Step 7: We write the equation as follows:
$latex (x-h)^2=-k$
Step 8: We take the square root of both sides of the equation:
$latex x-h=\sqrt{-k}$
Step 9: The solutions of the quadratic equation are:
$latex x=h\pm \sqrt{-k}$
Solving quadratic equations by completing the square – Examples with answer
The technique of completing the square is used to solve the following examples. The steps seen above are applied, but in a more simplified way.
EXAMPLE 1
Complete the square of the expression $latex x^2+2x-3=0$ and solve the equation.
Solution
Since the value of the coefficient a is equal to 1, we don’t have to divide the equation by any numbers initially.
The coefficient b is equal to 2. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{2}{2}\right)^2=1$$
Adding and subtracting that value, we have:
$$x^2+2x-3=x^2+2x+1-1-3$$
Completing the square and simplifying, we have:
$latex = (x+1)^2-1-3$
$latex = (x+1)^2-4$
Now, we can write the equation as follows:
$latex (x+1)^2=4$
And we take the square root of both sides:
⇒ $latex x+1=\pm 2$
Solving, we have:
⇒ $latex x=1~~$ or $latex ~~x=-3$
EXAMPLE 2
Solve the equation $latex x^2+4x-6=0$ using the method of completing the square.
Solution
We don’t have to apply the first step, since the coefficient of the term is equal to 1.
Here, the coefficient b is equal to 4. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Adding and subtracting that value to the quadratic equation, we have:
$$x^2+4x-6=x^2+4x+2^2-2^2-6$$
Completing the square and simplifying, we have:
$latex = (x+2)^2-4-6$
$latex = (x+2)^2-10$
Therefore, we have the equation:
$latex (x+2)^2=10$
Taking the square root of both sides, we have:
⇒ $latex x+2=\sqrt{10}$
Solving, we have:
⇒ $latex x=-2\pm \sqrt{10}$
EXAMPLE 3
Solve the quadratic equation $latex x^2+6x-1=0$ by completing the square.
Solution
In this equation, we have a coefficient b equal to 3, so we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{6}{2}\right)^2$$
$$=3^2$$
Adding and subtracting that value to the quadratic expression, we have:
$$x^2+6x-1=x^2+6x+3^2-3^2-1$$
Completing the square and simplifying, we have:
$latex = (x+3)^2-9-1$
$latex = (x+3)^2-10$
To solve the equation, we write it as follows:
$latex (x+3)^2=10$
Taking the square root of both sides, we have:
⇒ $latex x+3=\sqrt{10}$
Solving, we have:
⇒ $latex x=-3\pm \sqrt{10}$
EXAMPLE 4
Complete the square of the expression $latex 2x^2+8x-10=0$ and solve the equation.
Solution
We start by dividing the expression by 2 to make the coefficient of the quadratic term equal to 1:
⇒ $latex x^2+4x-5=0$
Now, the coefficient b is equal to 4. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Adding and subtracting to the quadratic expression, we have:
$$x^2+4x-5=x^2+4x+2^2-2^2-5$$
We complete the square and simplify
$latex = (x+2)^2-4-5$
$latex = (x+2)^2-9$
Now, we write the equation like this:
⇒ $latex (x+2)^2=9$
And we take the square root of both sides:
⇒ $latex x+2=\pm 3$
Solving, we have:
⇒ $latex x=1~~$ or $latex ~~x=-5$
EXAMPLE 5
Use the method of completing the square to solve the equation $latex x^2-3x+1=0$.
Solution
The coefficient b in this equation is equal to -3. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{-3}{2}\right)^2$$
Adding and subtracting this expression to the quadratic equation, we have:
$$x^2-3x+1=x^2-2x+\left(\frac{-3}{2}\right)^2-\left(\frac{-3}{2}\right)^2+1$$
Completing the square and simplifying, we have:
$latex = (x-\frac{3}{2})^2-\left(\frac{-3}{2}\right)^2+1$
$latex = (x-\frac{3}{2})^2-\frac{5}{4}$
Now, we can write the equation as follows:
$latex ⇒ (x-\frac{3}{2})^2=\frac{5}{4}$
Taking the square root of both sides, we have:
⇒ $latex x-\frac{3}{2}=\sqrt{\frac{5}{4}}$
⇒ $latex x-\frac{3}{2}=\frac{\sqrt{5}}{2}$
Solving, we have:
⇒ $latex x=\frac{3}{2}\pm \frac{\sqrt{5}}{2}$
EXAMPLE 6
Find the solutions to the equation $latex x^2+6x-7=0$ using the method of completing the square.
Solution
In this equation, the coefficient b is equal to 6. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{6}{2}\right)^2$$
$$=3^2$$
Adding that expression to the quadratic equation, we have:
$$x^2+6x-7=x^2+6x+3^2-3^2-7$$
Completing the square and simplifying, we have:
$latex = (x+3)^2-9-7$
$latex = (x+3)^2-16$
Now, we can write the equation as follows:
$latex (x+3)^2=16$
We take the square root of both sides to solve:
$latex x+3=\pm 4$
⇒ $latex x=1~~$ or $latex ~~x=-7$
EXAMPLE 7
Solve the quadratic equation $latex 3x^2+15x+15=0$ using the method of completing the square.
Solution
We start by dividing the equation by 3 to make the coefficient of the quadratic term equal to 1:
$latex x^2+3x+3=0$
Here, the coefficient b is equal to 3. Therefore, we have:
$$\left(\frac{b}{2}\right)^2=\left(\frac{3}{2}\right)^2$$
Adding and subtracting this value to the quadratic expression, we have:
$$x^2+3x+3=x^2+3x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+3$$
Completing the square and simplifying, we have:
$latex = (x+\frac{3}{2})^2-\frac{9}{4}+3$
$latex = (x+\frac{3}{2})^2+\frac{3}{4}$
Now, we write as follows:
$latex = (x+\frac{3}{2})^2=-\frac{3}{4}$
Taking the square root of both sides, we have:
$latex (x+\frac{3}{2})=\sqrt{-\frac{3}{4}}$
Since $latex \sqrt{-\frac{3}{4}}$ is not a real number, the equation has no real roots.
Solving quadratic equations by completing the square – Practice problems
Use the technique of completing the square to solve the following quadratic equations. Click “Check” to make sure that you got the correct answer.
See also
Interested in learning more about completing the square? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
