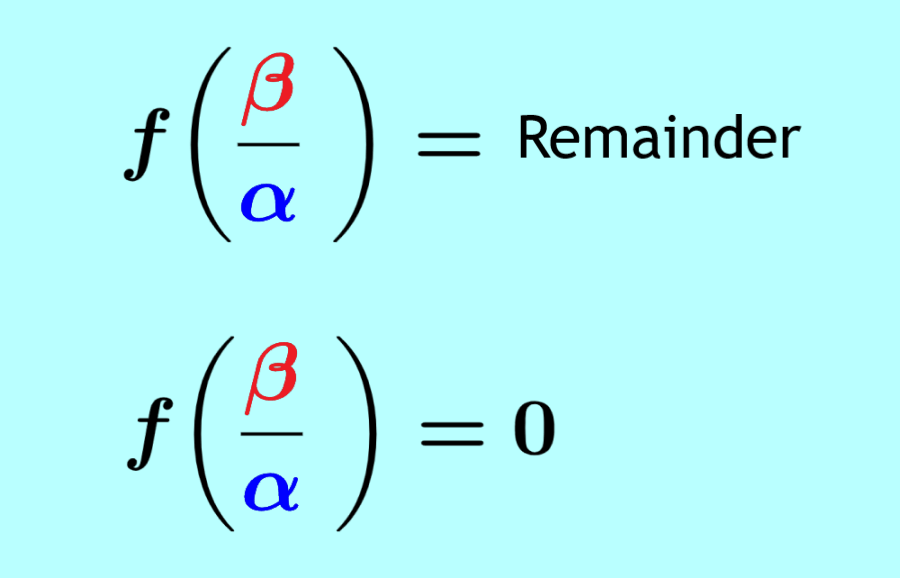The remainder and factor theorems are two algebraic theorems related to the division and factorization of polynomials. The remainder theorem allows us to find the remainder when we divide a polynomial by a linear expression. On the other hand, the factor theorem allows us to verify the factors of a polynomial.
Here, we will learn everything related to the remainder and factor theorems. We will look at their statements, the proofs of the theorems, and some examples.
What is the remainder theorem?
The remainder theorem is an algebraic theorem stating that when we divide a polynomial $latex f(x)$ by $latex (\alpha x-\beta)$, the remainder is $latex f\left(\frac{\beta }{\alpha}\right)$.
This means that we can use the Remainder Theorem to find the remainder when dividing a polynomial by the expression $latex (\alpha x-\beta)$.
Proof of the remainder theorem
The result of a division is the quotient. Therefore, if we multiply the quotient by the divisor and add the remainder, we get the original polynomial. That is, we have:
$$f(x)=(\alpha x-\beta)(\text{Quotient})+(\text{Remainder})$$
Now, we are going to use the value $latex x=\frac{\beta}{\alpha}$, to obtain the following:
$$f\left(\frac{\beta}{\alpha}\right)=\left[ \alpha \left(\frac{\beta}{\alpha}\right)-\beta\right](\text{Quotient})+(\text{Remainder})$$
$$=\left[ \beta-\beta\right](\text{Quotient})+(\text{Remainder})$$
$$=\left[ 0 \right](\text{Quotient})+(\text{Remainder})$$
$$=\text{Remainder}$$
We see that the Remainder Theorem is true since by using $latex x=\frac{\beta}{\alpha}$ in the function, we get the remainder of the division.
What is the factor theorem?
The factor theorem is an algebraic theorem that tells us that if $latex (\alpha x-\beta)$ is a factor of the polynomial $latex f(x)$, then $latex f\left(\frac{ \beta}{\alpha}\right)=0$.
This means that the factor theorem connects the factors and the zeros of a polynomial. The remainder theorem can be considered as a specific version of this theorem.
Additionally, we can use the factor theorem to remove known zeros from a polynomial and leave all unknown zeros intact, resulting in a lower-degree polynomial with easier zeros to find.
Proof of the factor theorem
If $latex (\alpha x-\beta)$ is a factor of $latex f(x)$, then the remainder equals 0 when we divide $latex f(x)$ by $latex (\alpha x -\beta)$.
Therefore, if we use the Remainder Theorem, we can show that
$$f\left(\frac{\beta}{\alpha}\right)=0$$
How to use the factor theorem:
The following are the steps that we can follow to use the factor theorem and identify the factors of a polynomial:
Step 1: If $latex f(-c)=0$, then $latex (x+ c)$ is a factor of the polynomial $latex f(x)$.
Step 2: If $latex p(\frac{d}{c})= 0$, then $latex (cx-d)$ is a factor of the polynomial $latex f(x)$.
Step 3: If $latex p(-\frac{d}{c})= 0$, then $latex (cx+d)$ is a factor of the polynomial $latex f(x)$.
Step 4: If $latex p(c)=0$ and $latex p(d) =0$, then $latex (x – c)$ and $latex (x -d)$ are factors of the polynomial $latex p(x)$.
The factor theorem can be an easier method for finding the factors of a polynomial as opposed to the long division method. We can use this theorem to remove known zeros while leaving all unknown zeros intact in order to find the lower-degree polynomial.
If the remainder is zero, the factor theorem is shown as follows:
If $latex f(c)=0$, the polynomial $latex f(x)$ has a factor $latex (x-c)$, where $latex f(x)$ is a polynomial of degree $latex n$.
Examples of the remainder and factor theorems
The following examples are solved by applying the remainder and factor theorems. Each example has a detailed solution.
EXAMPLE 1
Find the remainder when we divide the polynomial $latex x^3+5x^2-17x-21$ by $latex x-4$.
Solution: To solve this, we have to use the Remainder Theorem.
The Remainder Theorem tells us that when $latex f(x)$ is divided by $latex x-4$, it is $latex f(4)$. Therefore, we have:
$$f(4)=(4)^3+5(4)^2-17(4)-21$$
$latex =64+80-68-21$
$latex =55$
The remainder of the division is 55.
EXAMPLE 2
When we divide the polynomial $latex 3x^3+bx^2-7x+5$ by $latex x+3$, the remainder is 17. Find the value of b.
Solution: In this case, we are going to use the Remainder Theorem to form an equation and then solve for b.
Using the remainder theorem, we know that $latex f(-3)=17$. Thus, we have:
$$3(-3)^3+b(-3)^2-7(-3)+5=17$$
$latex -81+9b+21+5=17$
$latex 9b=72$
$latex b=8$
The value of b is 8.
EXAMPLE 3
Determine if $latex (x+1)$ is a factor of the polynomial $latex f(x) = {x}^2 + x – 2$.
Solution: To determine if $latex (x+1)$ is a factor, we are going to use the factor theorem.
The factor theorem tells us that if x+1 is a factor of the polynomial, we must have $latex f(-1)=0$. Therefore, using $latex x=-1$ in the polynomial, we have:
$latex f(x) = {x}^2 – x -2$
$latex f(-1) = {(-1)}^2 – (-1) -2$
$latex f(-1) = 1 +1 – 2 $
$latex f(-1) = 0$
We see that f(-1) = 0. This means that $latex (x + 2)$ is a factor of the given polynomial.
EXAMPLE 4
Is $latex (2x-1)$ a factor of the polynomial $latex f(x) = 2{x}^2 – x – 1$?
Solution: Again, we are going to use the factor theorem to solve this.
If 2x-1 is a factor of the polynomial, we should have $latex f(\frac{1}{2})=0$. Substituting the value $latex \frac{1}{2}$ into the polynomial, we have:
$latex f(\frac{1}{2}) = 2{x}^2 – x – 1$
$latex f(\frac{1}{2}) = 2{(\frac{1}{2})}^2 – (\frac{1}{2}) – 1$
$latex f(\frac{1}{2}) = 2(\frac{1}{4}) – (\frac{1}{2}) – 1$
$latex f(\frac{1}{2}) = \frac{1}{2} – (\frac{1}{2}) – 1$
We got $latex f(\frac{1}{2}) = -1$. This means that (2x–1) is not a factor of $latex f(x) = 2{x}^2 – x – 1$.
See also
Interested in learning more about the remainder and factor theorems? You can take a look at these pages: