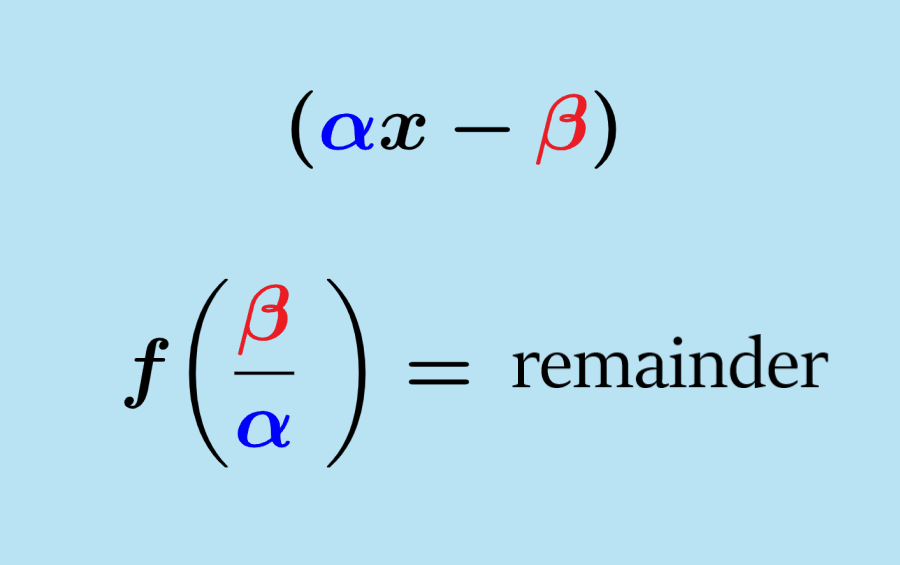The remainder theorem tells us that when a polynomial f(x) is divided by (αx–β), the remainder is equal to f(β/α). This means that to find the remainder of the division, we have to evaluate the function using the β/α value, that is, the x value of the factor (the divisor).
Below, we will look at 10 examples with answers of the remainder theorem. In addition, you will be able to test your skills with some practice problems.
10 Examples of the Remainder Theorem with answers
The following examples are solved by applying the Remainder Theorem. Each example has its respective solution, but try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the remainder when the polynomial $latex x^3+4x^2+7x+6$ is divided by $latex x+2$?
Solution
To find the remainder, we can use the Remainder Theorem. This theorem tells us that the remainder of the division is $latex f\left(\frac{\beta}{\alpha}\right)$.
In this case, we have $latex f\left(\frac{\beta}{\alpha}\right)=f(-2)$. Thus, we have:
$$f(-2)=(-2)^3+4(-2)^2+7(-2)+6$$
$latex =-8+16-14+6$
$latex =0$
We see that the remainder is equal to 0. This means that the division is exact.
EXAMPLE 2
If we now divide the polynomial $latex x^3+4x^2+7x+6$ by $latex x-4$, what is the remainder?
Solution
Using the remainder theorem we know that the remainder when $latex f(x)$ is divided by $latex x-4$ is $latex f(4)$. Therefore, we have:
$$f(4)=(4)^3+4(4)^2+7(4)+6$$
$latex =64+64+28+6$
$latex =162$
The remainder of the division is 162.
EXAMPLE 3
Find the remainder when $latex x^3+4x^2-5x+10$ is divided by $latex x+5$.
Solution
To solve this, we can use the Remainder Theorem, which tells us that when $latex f(x)$ is divided by $latex x+5$ it is $latex f(5)$. Therefore, we have:
$$f(-5)=(-5)^3+4(-5)^2-5(-5)+10$$
$latex =-125+100+25+10$
$latex =10$
The remainder of the division is 10.
EXAMPLE 4
Find the remainder when $latex x^3-5x^2+4x+2$ is divided by $latex (2x+1)$.
Solution
The remainder theorem tells us that the remainder when $latex f(x)$ is divided by $latex 2x+1$ is $latex f\left(-\frac{1}{2}\right)$. Thus, we have:
$$f\left(-\frac{1}{2}\right)=\left(-\frac{1}{2}\right)^3-5\left(-\frac{1}{2}\right)^2+4\left(-\frac{1}{2}\right)+2$$
$latex =-\frac{1}{8}-\frac{5}{4}-2+2$
$latex =-\frac{11}{8}$
The remainder of the division is $latex -\frac{11}{8}$.
EXAMPLE 5
What is the remainder when $latex 2x^3-2x^2+3x-10$ is divided by $latex (2x-3)$?
Solution
Using the remainder theorem, we know that when $latex f(x)$ is divided by $latex 2x-3$ the remainder is $latex f\left(\frac{3}{2}\right)$. Therefore, we have:
$$f\left(\frac{3}{2}\right)=\left(\frac{3}{2}\right)^3-2\left(\frac{3}{2}\right)^2+3\left(\frac{3}{2}\right)-10$$
$latex =\frac{27}{8}-\frac{9}{2}+\frac{9}{2}-10$
$latex =-\frac{73}{8}$
The remainder of the division is $latex -\frac{73}{8}$.
EXAMPLE 6
Determine the remainder when the polynomial $latex 5x^3-3x^2+4x-10$ is divided by x.
Solution
In this case, we just have x. Comparing with $latex (\alpha x-\beta)$, we see that $latex \beta$ is equal to 0. Therefore, we use $latex f\left(\frac{\beta}{\alpha}\right)= f(0)$ to find the remainder:
$$f(0)=5(0)^3-3(0)^2+4(0)-10$$
$latex =0-0+0-10$
$latex =-10$
The remainder of the division is -10.
EXAMPLE 7
When we divide the polynomial $latex 3x^3+bx^2-7x+5$ by $latex x+3$, we get a remainder of 17. What is the value of b?
Solution
We can solve this using the Remainder Theorem. Using the remainder theorem, we know that $latex f(-3)=17$. Thus, we form an equation and solve for b:
$$3(-3)^3+b(-3)^2-7(-3)+5=17$$
$latex -81+9b+21+5=17$
$latex 9b=72$
$latex b=8$
The value of b is 8.
EXAMPLE 8
The polynomial $latex 2x^3+3x^2-cx-2$ gives us a remainder of 10 when divided by $latex x-2$. Find the value of c.
Solution
Using the remainder theorem, we know that $latex f(2)=10$. Therefore, we form an equation and solve for c:
$$2(2)^3+3(2)^2-c(2)-2=10$$
$latex 16+12-2c-2=10$
$latex 2c=16$
$latex c=8$
The value of c is 8.
EXAMPLE 9
The remainder when $latex cx^3+2x^2-5x+7$ is divided by $latex x-2$ is equal to the remainder when the same expression is divided by $latex x+1$. Find the value of c.
Solution
Using the remainder theorem, we know that $latex f(2)=r$, where r is the remainder. Also, since the remainder is the same when we divide by $latex x+1$, we also have $latex f(-1)=r$.
Therefore, we can form an equation with $latex f(2)=f(-1)$ and then solve for c:
$$c(2)^3+2(2)^2-5(2)+7=c(-1)^3+2(-1)^2-5(-1)+7$$
$$8c+8-10+7=-c+2+5+7$$
$latex 9c=9$
$latex c=1$
The value of c is equal to 1.
EXAMPLE 10
When we divide the polynomial $latex f(x)=x^3+ax^2+bx+2$ by $latex x-1$, the remainder is 4 and when we divide it by $latex x+2$, the remainder is also is 4. Find the values of a and b.
Solution
Using the Remainder Theorem, we know that $latex f(1)=4$. Therefore, we have:
$$(1)^3+a(1)^2+b(1)+2=4$$
$latex 1+a+b+2=4$
$latex a+b=1$
Now, we use the remainder theorem with $latex f(-2)=4$ and we have:
$$(-2)^3+a(-2)^2+b(-2)+2=4$$
$latex -8+4a-2b+2=4$
$latex 4a-2b=10$
We can divide the last equation we obtained by 2 to simplify it:
$latex 2a-b=5$
Finally, we can solve by forming a system of equations with the two equations found. Solving, we get $latex a=2$ and $latex b=-1$.
5 Practice problems of the remainder theorem
Apply everything you have learned about the Remainder Theorem to solve the following practice problems.
See also
Interested in learning more about the remainder and factor theorems? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
