Piecewise functions are functions that have a different expression for different intervals in their domain. These functions can be thought of as functions composed of different pieces of two or more functions.
In this article, we will see a more detailed definition of these functions and we will learn how to obtain their graphs.
What is a piecewise function?
Piecewise functions are functions that are defined by different formulas or functions for each interval. As the name implies, these functions are defined by chunks of functions for each part of the domain.
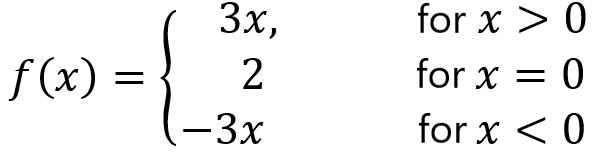
In the function above, we can see that f(x) is a piecewise function since it is defined differently for the three intervals x> 0, x = 0, and x <0. We can interpret piecewise functions by looking at the different given intervals. The function f (x) given above can be read as:
- When x> 0, f(x) is equal to 3x.
- When x = 0, f(x) is equal to 2,
- When x <0, f(x) equals -3x.
These changes can be clearly observed in the graph of the function:
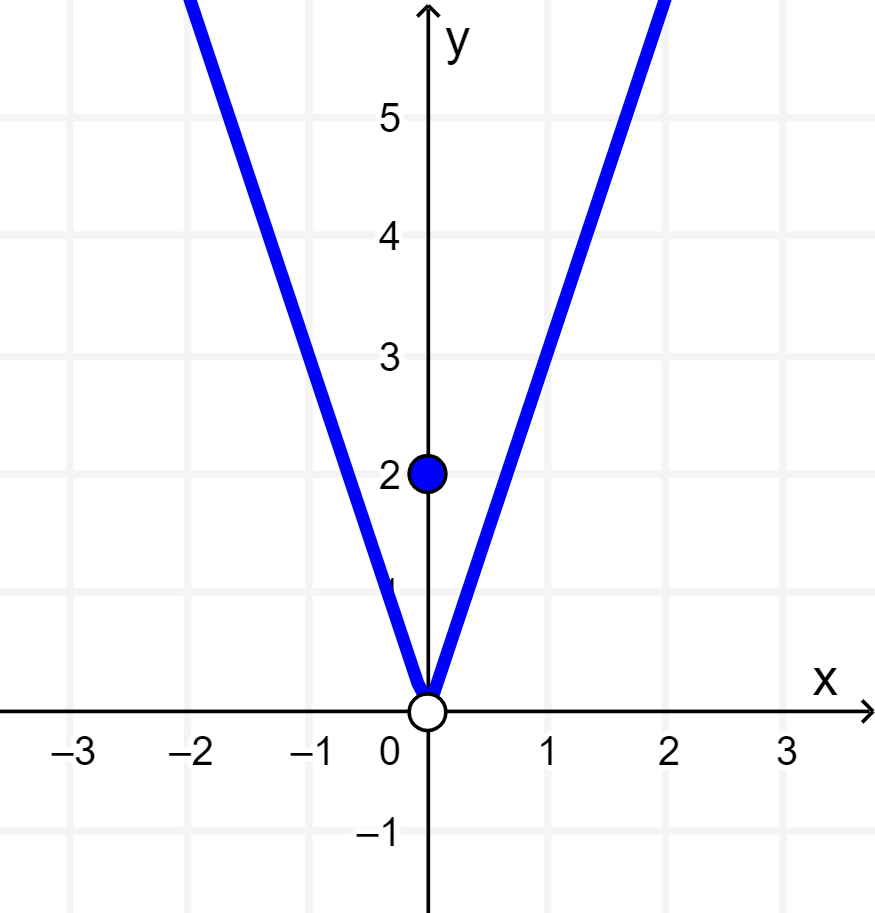
How to solve piecewise defined functions?
Now that we have learned a bit about these functions, we need to learn how to solve piecewise functions.
To solve piecewise functions, we have to take into account the following:
- Check carefully where the x lies in the given interval.
- Evaluate the value using the corresponding function.
For example, let’s say we want to find f(5) in the following function:
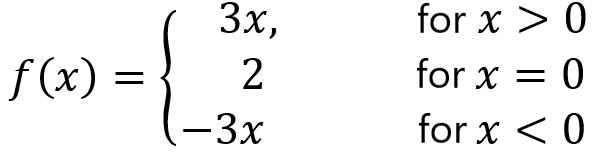
Since 5 is greater than 0, the function with which we will use to evaluate f (5) is f(x) = 3x. Therefore, we have f(5) = 3 (5) = 15.
This also means that we have f(0) = 2 and also f(-1) = -3 (-1) = 3.
How to graph piecewise functions?
To graph piecewise functions, we have to consider that each interval will have a different graph since the function is different in each interval.
We can take into account the following recommendations when graphing piecewise functions:
- We can think about how each function will look individually.
- For inclusive intervals (such as x≥0), we include the end points using filled points.
- For exclusive intervals (such as x> 0), we exclude the end points with empty points.
Some of the more common functions we can expect are the following:
- Constant functions like f(x) = 4.
- Linear functions like f(x) = 3x+1.
- Quadratic functions like f(x) = 2x²+x-3.
You can explore more types of functions and their graphs in our article on types of functions. This will help you get an idea of what we can expect each individual graph to look like.
Now, let’s graph the following function as an example:
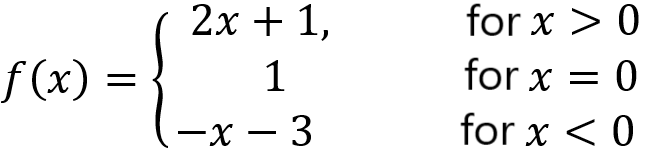
When we have x>0, and x<0, the function returns a linear expression. We can graph these linear parts simply by using two points that satisfy these expressions and drawing a line through the points taking into account that f(x) = 2x+1 only corresponds to values of x greater than 0 and that f(x) = –x-3, only corresponds to values of x less than 0. Since both are exclusive inequalities, we have an empty point at their endpoints:
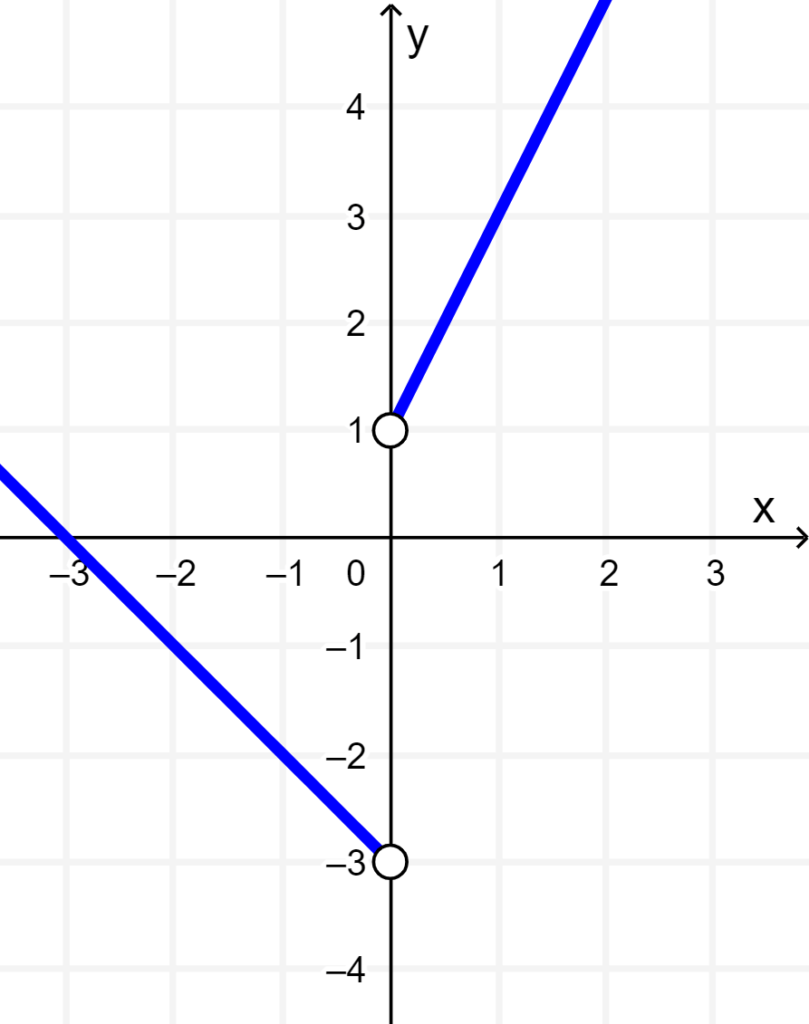
Now, we only have to complete the condition when x = 0. Since the value is constant at f(x) = 1, we can graph the point (0, 1):
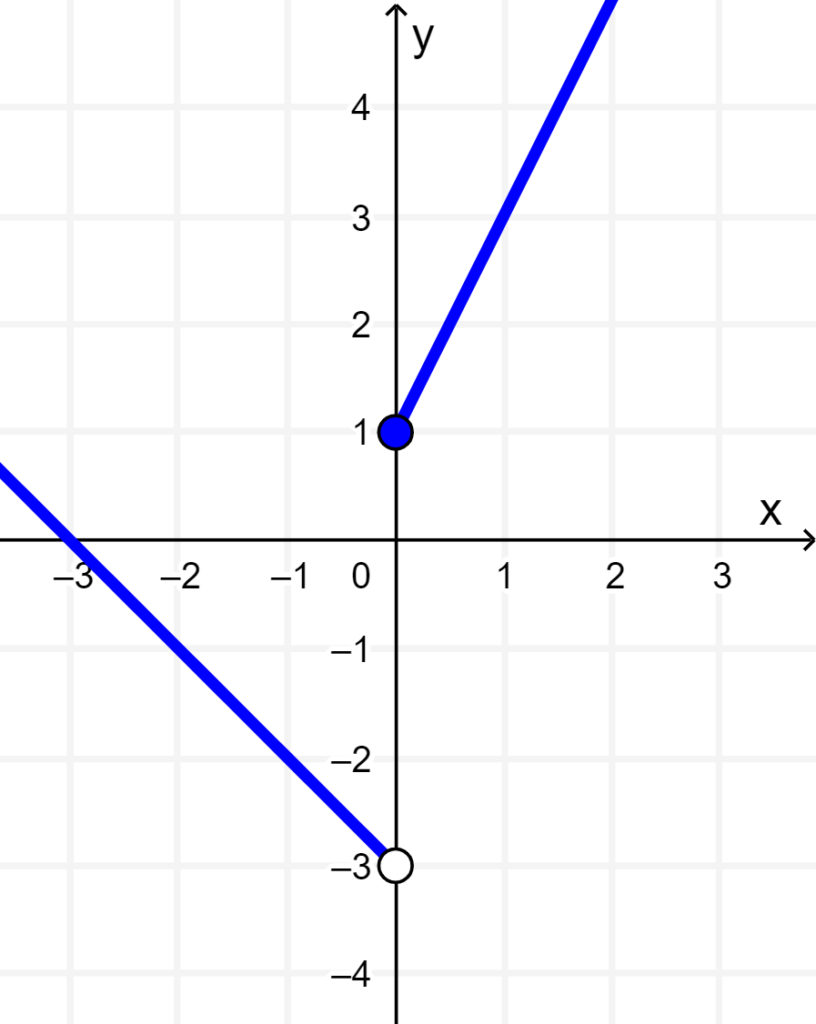
This is the final graph of this piecewise function. In the graph, we can see that the function has a domain of (-∞, ∞) and a range of (-3, ∞).
See also
Interested in learning more about functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
