Floor and ceiling functions are two important functions that are used frequently in mathematics and computing. The floor function assigns to each input an integer number that is equal or less than the input. The ceiling function assigns to each input an integer number that is equal or greater than the input.
In this article, we will look at more detailed definitions of these functions. We will also learn about their properties. Finally, we will look at their graphs along with several examples with answers.
Definition of floor and ceiling functions
Definition of ceiling function
A ceiling function is a function in which the smallest successive integer is returned. In other words, the ceiling function of a real number x is the smallest integer that is greater than or equal to the number x.
The notation used to represent the ceiling function is $latex \lceil ~ \rceil$. Therefore, the ceiling function is written as $latex f(x)=\lceil x \rceil$.
Definition of floor function
The floor function is defined as a function that returns the largest integer that is less than or equal to x. The notation used to represent the floor function is $latex \lfloor ~ \rfloor$. Therefore, the floor function is written as $latex f(x)=\lfloor x \rfloor$.
EXAMPLES
- $latex \lceil 2.5 \rceil=3$
- $latex \lfloor 2.5 \rfloor=2$
- $latex \lceil 4.85 \rceil=5$
- $latex \lfloor 4.85 \rfloor=4$
Properties of floor and ceiling functions
The floor and ceiling functions have many useful and interesting properties. The following are some of the most important. Here, n is an integer:
- $latex \lfloor x \rfloor=n$ only if $latex n\leq x<n+1$
- $latex \lceil x \rceil=n$ only if $latex n-1<x\leq n$
- $latex \lfloor x \rfloor=n$ only if $latex x-1< n\leq x$
- $latex \lceil x \rceil=n$ only if $latex x\leq n<x+1$
- $latex \lceil -x \rceil=-\lceil x \rceil$
- $latex \lfloor -x \rfloor=-\lfloor x \rfloor$
- $latex \lceil x+n \rceil=\lceil x \rceil +n$
- $latex \lfloor x+n \rfloor=\lfloor x \rfloor +n$
Formulas of floor and ceiling functions
Ceiling function formula
The formula to find the ceiling value for any specified value is:
$latex f(x)=$ minimum {$latex a \in Z; a \geq x$}
This means that the function returns the minimum integer that is greater than or equal to x. This is represented by:
$latex f(x)=<\lceil x \rceil =$ smallest successive integer of x
Floor function formula
The formula to find the floor value for any specified value is:
$latex f(x)=$ minimum {$latex a \in Z; a \geq x$}
This means that the function returns the maximum integer that is less than or equal to x. This is represented by:
$latex f(x)= \lfloor x \rfloor =$ greatest successive integer of x
Graphs of floor and ceiling functions
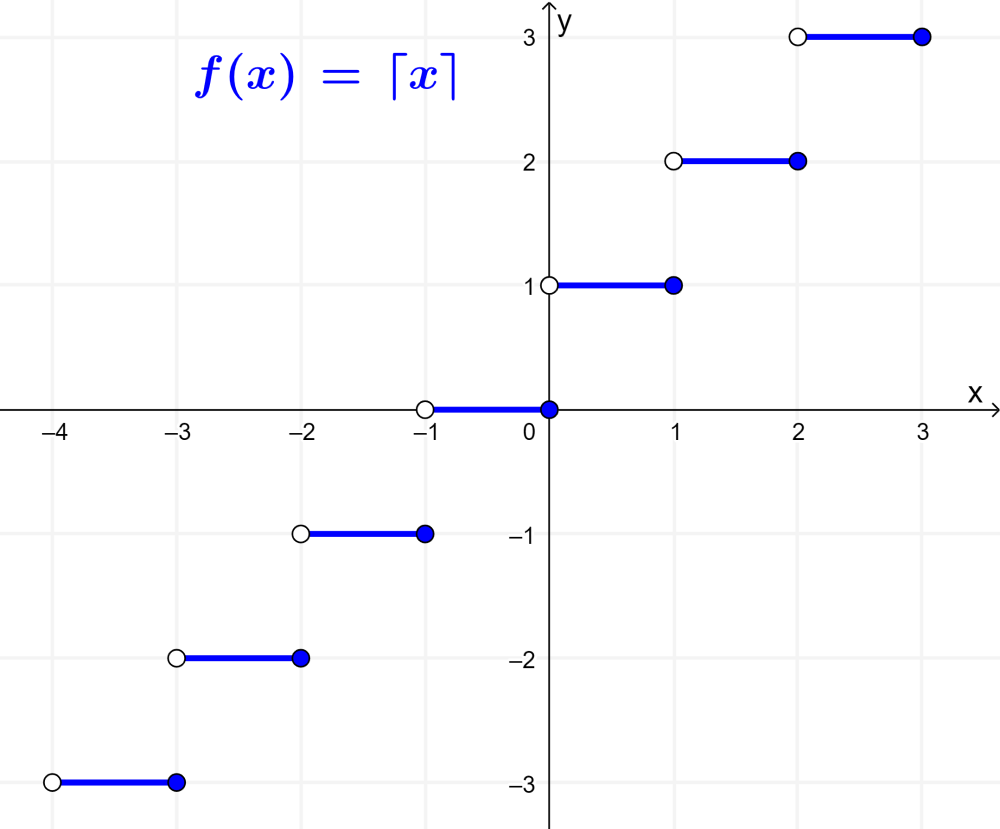
The graphs of the floor and ceiling functions have a shape that resembles stairs and have a discontinuity at each whole number point.
The following is the graph of the floor function:
The following is the graph of the ceiling function:
Floor and ceiling functions – Examples with answers
EXAMPLE 1
Apply the ceiling function to 3.4 and to -3.4.
Solution: We have $latex f(3.4)=\lceil 3.4 \rceil=4$ and $latex f(-3.4)=\lceil -3.4 \rceil=-3$.
The ceiling function of a real number is the smallest integer that is greater than or equal to x. In the case of 3.4, the larger integers are 4, 5, 6… The smallest of these is 4.
In the case of -3.4, the larger integers are -3, -2, -1, … The smallest of these is -3.
EXAMPLE 2
What is the result of $latex \lfloor \sqrt{46} \rfloor$?.
Solution: In this case, we have to find the largest integer that is equal to or less than $latex \sqrt{46}$.
We know that $latex \sqrt{36}<\sqrt{46}<\sqrt{49}$.
Therefore, we have $latex 6<\sqrt{46}<7$.
This means that, $latex \lfloor \sqrt{46} \rfloor=6$.
EXAMPLE 3
Solve the equation $latex \lfloor x-\frac{1}{2} \rfloor +\lfloor x-\frac{5}{2} \rfloor +\lfloor x-\frac{9}{2} \rfloor =3$.
Solution: We can solve this problem more easily by using the substitution $latex x-\frac{1}{2}=z$. Therefore, we have the equation:
$latex \lfloor z \rfloor +\lfloor z-2 \rfloor +\lfloor z-4 \rfloor =3$
Using the identity $latex \lfloor x+n \rfloor =\lfloor x \rfloor +n$, we have the following:
$latex \lfloor z \rfloor +\lfloor z \rfloor -2+\lfloor z \rfloor -4=3$
⇒ $latex 3\lfloor z \rfloor =9$
⇒ $latex \lfloor z \rfloor =3$
The last equation means that $latex 3\leq z<4$. When returning to the variable x, we have:
$latex 3\leq x-\frac{1}{2}<4$
⇒ $latex 3\frac{1}{2}\leq x<4\frac{1}{2}$
⇒ $latex x\in[3.5, 4.5)$
Floor and ceiling functions – Practice problems
See also
Interested in learning more about functions? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
