The equation of a line is an equation that satisfies and represents each of the points on the line. The equation of a line can be found using various methods depending on the information we have available.
In this article, we will learn about the equation of a line in its point-slope form. We will look at several examples with answers to practice the application of this equation and fully understand the concepts.
What is the equation of a line in point-slope form?
The formula of the equation of a line in its point-slope form is used to find the equation of a line. This formula is used only when we know the slope of the line and a point through which the line passes.
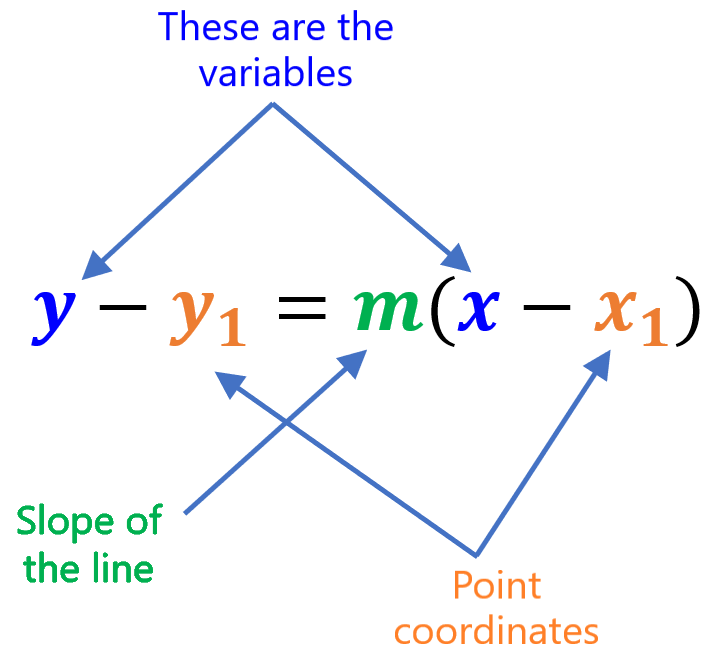
Then, the equation of a line that has slope m and which passes through the point $latex (x_{1}, ~ y_{1})$ is found using this form. The equation of the point-slope form is:
| $latex y-y_{1}=m(x-x_{1})$ |
where, $latex (x_{1}, ~y_{1})$ is any point that is located on the line.
Linear equations in point-slope form – Examples with answers
The point-slope form is applied to find the answer to the following examples. These examples have a detailed solution that helps us understand the use of the formula. Try to solve the examples yourself before looking at the solution.
EXAMPLE 1
Find the equation of the line that passes through the point (-3, 1) and has a slope of 2.
Solution
The given point that passes through the line is:
$latex (x_{1},~y_{1})=(-3, ~1)$
The slope of the line is:
$latex m=2$
We find the equation of the line using the point slope formula:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=2(x-(-3))$
$latex y-1=2(x+3)$
$latex y-1=2x+6$
$latex y=2x+7$
Therefore, the equation of the line is:
$latex y=2x+7$
EXAMPLE 2
Find the equation of the line that has a slope of -1 and passes through the point (2, 1).
Solution
The given point that passes through the line is:
$latex (x_{1},~y_{1})=(2, ~1)$
The slope of the line is:
$latex m=-1$
We use the point slope formula to find the equation of the line:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=-1(x-2)$
$latex y-1=-x+2$
$latex y=-x+3$
Therefore, the equation of the line is:
$latex y=-x+3$
EXAMPLE 3
Find the equation of the line that has a slope of $latex \frac{1}{2}$ and passes through point (-4, 3).
Solution
We have that the following point passes through the line:
$latex (x_{1},~y_{1})=(-4, ~3)$
The slope of the line is:
$latex m=\frac{1}{2}$
We use the point slope formula to find the equation of the line:
$latex y-y_{1}=m(x-x_{1})$
$latex y-3=\frac{1}{2}(x-(-4))$
$latex y-3=\frac{1}{2}(x+4)$
$latex y-3=\frac{1}{2}x+2$
$latex y=\frac{1}{2}x+5$
Therefore, the equation of the line is:
$latex y=\frac{1}{2}x+5$
EXAMPLE 4
Find the equation of the line that passes through the point (3, 1) and has a slope of $latex -\frac{2}{3}$.
Solution
We have that the following point passes through the line:
$latex (x_{1},~y_{1})=(3, ~1)$
The slope of the line is:
$latex m=-\frac{2}{3}$
We find the equation of the line using the point-slope form:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=-\frac{2}{3}(x-3)$
$latex y-1=-\frac{2}{3}(x-2)$
$latex y-1=-\frac{2}{3}x+2$
$latex y=-\frac{2}{3}x+3$
Therefore, the equation of the line is:
$latex y=-\frac{2}{3}x+3$
EXAMPLE 5
Find the equation of a horizontal line that passes through the point (2,1).
Solution
We know that the slope of a horizontal line is $latex m=0$.
The line passes through the point $latex (x_{1}, ~y_{1})=(2, 1)$.
The equation of the line using the point-slope form is:
$latex y-y_{1}=m(x-x_{1})$
$latex y-1=0(x-2)$
$latex y-1=0$
$latex y=1$
Then, the equation of the horizontal line is:
$latex y=1$
EXAMPLE 6
Which of the following graphs could represent the equation $latex y+1=-3(x-2)$?
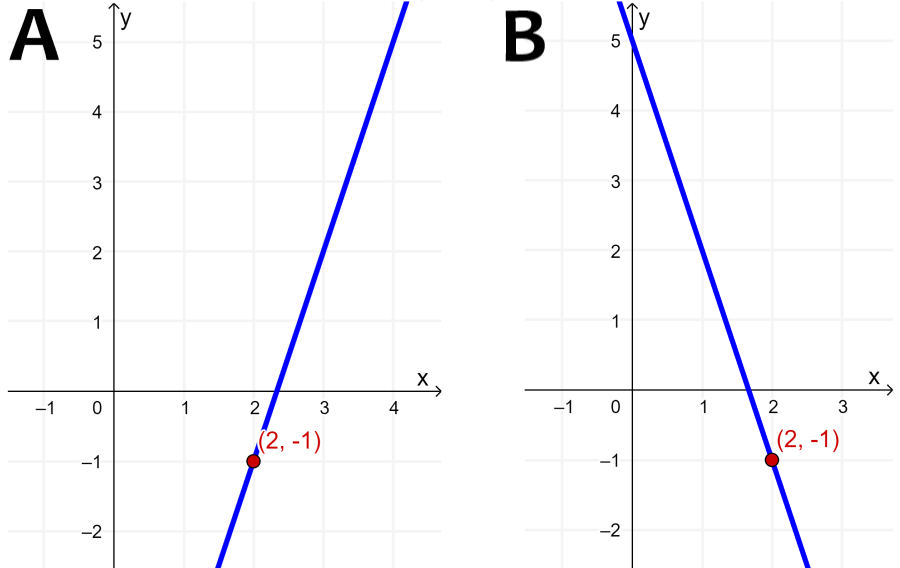
Solution
Relating the given equation $latex y+1=-3(x-2)$ with the point slope form of a line $latex y-y_{1}=m(x-x_{1})$, we have:
- $latex x_{1}=2$
- $latex y_{1}=-1$
- $latex m=-3$
Therefore, we have the point $latex (x_{1}, ~ y_{1}) = (2, ~ -1)$. We see that both graphs contain this point, so there is no difference there.
However, we have the slope $latex m = -3$ and we know that a negative slope has a downward slope, that is, the line decreases from left to right. This means that graph B is the correct graph of the equation.
Linear equations slope-intercept form – Practice problems
Test your knowledge of the point-slope form of a line with the following interactive problems. Select your answer and check it to see that you chose the correct one. You can look at the solved examples above if you have a problem with these exercises.
See also
Interested in learning more about linear equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
