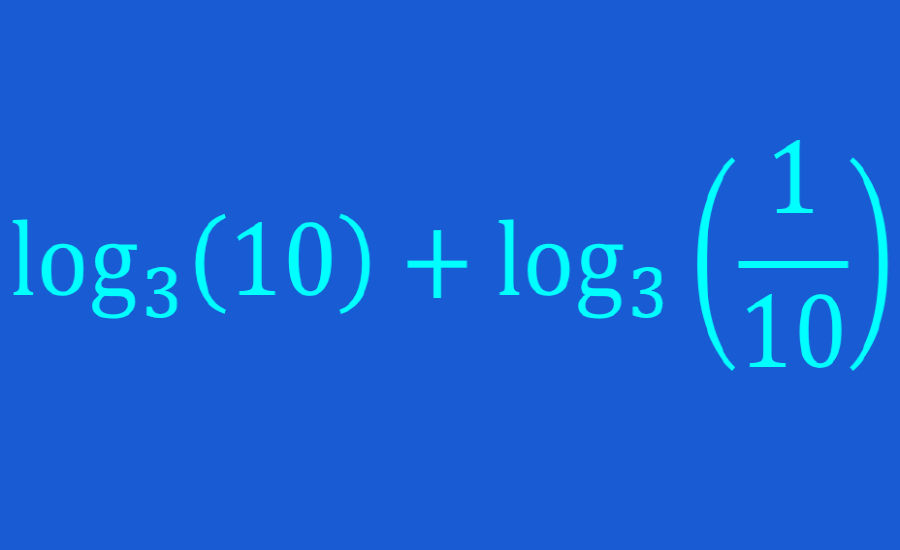Logarithmic expressions can be simplified, expanded, and solved using the laws of logarithms. The laws of logarithms tell us different ways in which a logarithmic expression can be written.
Here, we will look at a summary of the main laws of logarithms. In addition, we will look at several logarithm exercises with answers to learn how to apply the laws of logarithms to solve algebraic exercises.
Summary of the laws of logarithms
The logarithm of a number is the power to which the number has to be raised to obtain a specific value. For example, the base 2 logarithm of 8 is 3, since 2 raised to the power of 3 equals 8:
$latex \log_{2}(8)=3$
as:
$latex {{2}^3}=8$
The following are the most important logarithmic laws that can help us simplify or rewrite complex logarithmic expressions.
Product law
The logarithm of a product can be written as the sum of the logarithms of the individual factors:
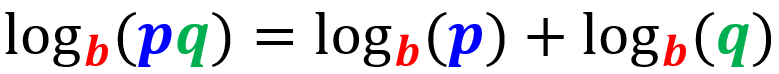
Quotient law
The logarithm of a quotient can be rewritten as the logarithm of the numerator minus the logarithm of the denominator:
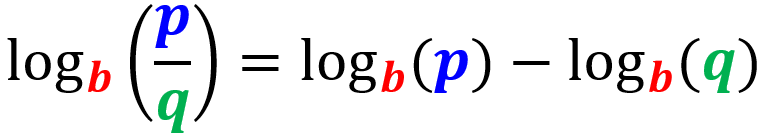
Power law
The logarithm of an exponential expression can be rewritten as the exponent multiplied by the logarithm of the base (without the exponent):
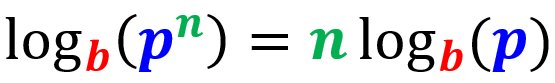
Zero law
The logarithm of 1, where the base is $latex b>0$, but $latex b \neq 0$, is equal to zero:
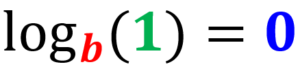
Identity law
The logarithm of a number equal to the base is equal to 1. We have that the argument is equal to the base, so b must be greater than zero, but it cannot be equal to 1:
Law of the logarithm of the exponent
When taking the logarithm of an exponential number with the same base of the logarithm, the result is the exponent:
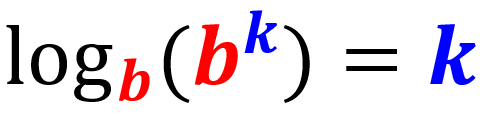
Law of the exponent of a logarithm
By having a number raised to a logarithm, where the base of the logarithm is equal to the base of the number, the result is the argument of the logarithm:
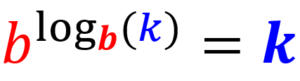
Problems with answers of logarithms
The following logarithm exercises are solved using the laws of logarithms summarized above. Each exercise has its respective solution, but it is recommended that you solve the exercises yourself before looking at the answer.
EXERCISE 1
Solve the following: $latex \log_{4}(8)+\log_{4}(8)$.
Solution
Using the law of the logarithm of a product, we have:
$latex \log_{4}(8)+\log_{4}(8)=\log_{4}(8\times 8)$
$latex =\log_{4}(64)$
Now, we can write the logarithm in its exponential form to get the exponent:
$latex 64={{4}^3}$
Therefore, the answer is 3.
EXERCISE 2
Solve the following expression: $latex \log_{5}(100)-\log_{5}(4)$.
Solution
We can apply the law of the logarithm of a quotient to form a single expression with the subtraction of logarithms:
$latex \log_{5}(100)-\log_{5}(4)=\log_{5}(\frac{100}{4})$
$latex =\log_{5}(25)$
Rewriting the expression in its exponential form, we can find the exponent:
$latex 25={{5}^2}$
Therefore, the answer is 2.
EXERCISE 3
What is the value of $latex \log_{\sqrt{2}}(64)$?
Solution
We start by writing 64 as an exponential and then we apply the power law:
$latex \log_{\sqrt{2}}(64)=\log_{\sqrt{2}}{{(2)}^6}$
$latex =6\log_{\sqrt{2}}(2)$
We can write 2 as an exponential and reuse the power law:
$latex =6\log_{\sqrt{2}}{{(\sqrt{2})}^2}$
$latex =6\times 2\log_{\sqrt{2}}(\sqrt{2})$
$latex =6\times 2(1)$
$latex =12$
EXERCISE 4
Evaluate the following expression: $$\log_{3}(108)-2\log_{3}(2)+\log_{5}(12.5)+\log_{5}(10)$$
Solution
We can simplify this expression by separating it into two parts. Let’s simplify logarithms base 3 and logarithms base 5 separately. Therefore, we are going to use the quotient law to simplify the logarithms base 3 and we are going to use the product law to simplify the logarithms base 5.
However, we have to start by applying the power law to the logarithm with base 3:
$$\log_{3}(108)-2\log_{3}(2)+\log_{5}(12.5)+\log_{5}(10)$$
$$=\log_{3}(108)-\log_{3}{{(2)}^2}+\log_{5}(12.5)+\log_{5}(10)$$
$$=\log_{3}(108)-\log_{3}(4)+\log_{5}(12.5)+\log_{5}(10)$$
$latex =\log_{3}(\frac{108}{4})+\log_{5}(12.5\times 10)$
$latex =\log_{3}(27)+\log_{5}(125)$
If we write the arguments as powers, we can apply the power law of logarithms:
$latex =\log_{3}({{3}^3})+\log_{5}({{5}^3})$
$latex =3\log_{3}(3)+3\log_{5}(5)$
$latex =3(1)+3(1)$
$latex =6$
EXERCISE 5
Simplify the following expression: $latex \log_{5}(500)-2\log_{5}(2)+\log_{6}(216)$.
Solution
We can apply the product law to logarithms with base 5 and we can apply the power law to the logarithm with base 6:
$latex \log_{5}(500)-2\log_{5}(2)+\log_{6}(216)$
$latex =\log_{5}(500)-\log_{5}({{2}^2})+\log_{6}(216)$
$latex =\log_{5}(500)-\log_{5}(4)+\log_{6}(216)$
$latex =\log_{5}(\frac{500}{4})+\log_{6}(216)$
$latex =\log_{5}(125)+\log_{6}(216)$
Now, we can rewrite the arguments as powers and apply the power law of logarithms:
$latex =\log_{5}({{5}^3})+\log_{6}({{6}^3})$
$latex =3\log_{5}(5)+3\log_{6}(1)$
$latex =3(1)+3(1)$
$latex =6$
EXERCISE 6
Simplify the logarithmic expression: $latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$.
Solution
We start by using the power law to rewrite logarithms. Then we will use the product law and the quotient law to form a single logarithm since all the bases are the same:
$latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$
$latex =\log_{3}({{5}^2})+\log_{3}(40)-\log_{3}({{10}^3})$
$latex =\log_{3}(25)+\log_{3}(40)-\log_{3}(1000)$
$latex =\log_{3}(\frac{25\times 40}{1000})$
$latex =\log_{3}(1)$
Now, we solve by applying the law of zero:
$latex \log_{3}(1)=0$
EXERCISE 7
What is the expanded version of the expression: $latex \log_{3}(27{{x}^2}{{y}^5})$.
Solution
We have a logarithm of a product of factors, so we can use the product law to separate the factors:
$$\log_{3}(27{{x}^2}{{y}^5})=\log_{3}(27)+\log_{3}({{x}^2})+\log_{3}({{y}^5})$$
Now, we can rewrite 27 as a power and apply the power law to all logarithms:
$latex =\log_{3}({{3}^3})+\log_{3}({{x}^2})+\log_{3}({{y}^5})$
$latex =3\log_{3}(3)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3(1)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3+2\log_{3}(x)+5\log_{3}(y)$
Logarithms – Practice problems
Test your knowledge of logarithms and the laws of logarithms to solve the following problems. If you need help with these problems, you can look at the laws of logarithms or the solved examples above.
See also
Interested in learning more about logarithms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
