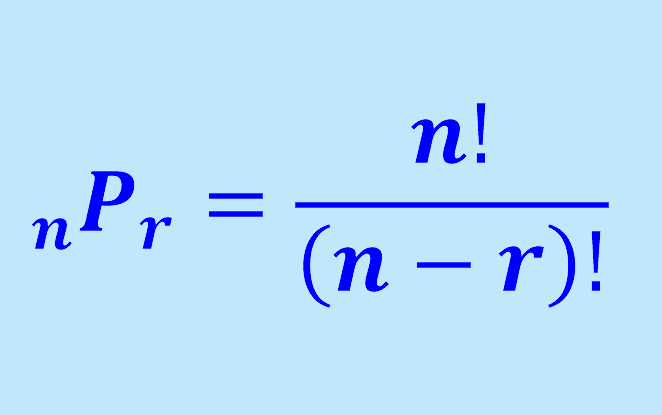With permutations, we can count the number of different ways of choosing objects from a set if the order of the objects does matter. This is different from combinations, where the order of the objects does not matter.
Here, we will start with a summary of permutations and look at their formula. Then, we will see several examples with answers to understand the application of the permutations formula.
Summary of permutations
A permutation is a list of objects, in which the order is important. Permutations are used when we are counting without replacing objects and order does matter. If the order doesn’t matter, we use combinations.
In general P(n, k) means the number of permutations of n objects from which we take k objects. Alternatively, the permutations formula is expressed as follows:
| $latex _{n}{{P}_{k}}=\frac{{n!}}{{( {n-k} )!}}$ |
where:
- n represents the total number of elements in a set
- k represents the number of selected objects
- ! is the factorial symbol
To solve permutations problems, we have to remember that the factorial (denoted as “!”) is equal to the product of all positive integers less than or equal to the number preceding the factorial. For example, $latex 4!=1 \times 2 \times 3 \times 4 = 24$.
Permutations – Examples with answers
In the following examples, we will see the application of the permutations formula. Each example has its respective detailed solution, which can be used to understand the reasoning in the answer to each exercise.
EXAMPLE 1
Find the result of the permutation $latex _{7}P_{3}$.
Solution
We have to use the permutations formula $latex _{n}{{P}_{k}}=\frac{{n!}}{{(n-k)!}}$, and substitute $latex n=7$ and $latex k=3$:
$latex _{7}{{P}_{3}}=\frac{{7!}}{{(7-3)!}}$
$latex =\frac{{7!}}{{(4)!}}$
We can simplify this by writing to 7! as $latex 7\times 6\times 5\times 4!$:
$latex\frac{{7!}}{{(4)!}}=\frac{{7\times 6\times 5\times 4!}}{{(4)!}}$
$latex =7\times 6\times 5=210$
EXAMPLE 2
Find the result of the permutation $latex _{8}P_{7}$.
Solution
We use the permutations formula $latex _{n}{{P}_{k}}=\frac{{n!}}{{(n-k)!}}$ using the values $latex n=8$ and $latex k=7$:
$latex _{8}{{P}_{7}}=\frac{{8!}}{{(8-7)!}}$
$latex =\frac{{8!}}{{(1)!}}$
In this case, we have nothing to simplify, so we have to calculate 8!:
$latex\frac{{8!}}{{(1)!}}=8!$
$latex =40 320$
EXAMPLE 3
Find the number of permutations $latex _{9}P_{6}$.
Solution
In this case, we have the values $latex n=9$ and $latex k=6$:
$latex _{9}{{P}_{9}}=\frac{{9!}}{{(9-6)!}}$
$latex =\frac{{9!}}{{(3)!}}$
We recognize that we can write 9! as $latex 9\times 8\times 7\times 6\times 5\times 4\times 3!$.Therefore, we simplify the 3!:
$latex\frac{{9!}}{{(3)!}}=\frac{{9\times 8\times 7\times 6\times 5\times 4\times 3!}}{{(3)!}}$
$latex =9\times 8\times 7\times 6\times 5\times 4=60480$
EXAMPLE 4
How many permutations are there with 4 objects and 2 places?
Solution
We can recognize the values $latex n=4$ and $latex k=2$. Therefore, we use the formula substituting these values:
$latex _{4}{{P}_{2}}=\frac{{4!}}{{(4-2)!}}$
$latex =\frac{{4!}}{{(2)!}}$
We rewrite the 4! as $latex 4\times 3\times 2!$ and we simplify:
$latex\frac{{4!}}{{(2)!}}=\frac{{4\times 3\times 2!}}{{(2)!}}$
$latex =4\times 3=12$
EXAMPLE 5
In how many ways can a president, treasurer, and secretary be chosen from 7 candidates?
Solution
The problem involves 7 candidates, of which we chose 3. Therefore, we have the values $latex n=7$ and $latex k=3$:
$latex _{7}{{P}_{3}}=\frac{{7!}}{{(7-3)!}}$
$latex =\frac{{7!}}{{(4)!}}$
Now, we write 7! as $latex 7\times 6\times 5\times 4!$. Then, we simplify the 4!:
$latex\frac{{7!}}{{(4)!}}=\frac{{7\times 6\times 5\times 4!}}{{(4)!}}$
$latex =7\times 6\times 5=210$
EXAMPLE 6
In how many ways can the first 3 places be awarded in a race with 5 participants?
Solution
We recognize the values $latex n=5$ and $latex k=3$:
$latex _{5}{{P}_{3}}=\frac{{5!}}{{(5-3)!}}$
$latex =\frac{{5!}}{{(2)!}}$
We rewrite the factorial 5! as $latex 5 \times 4 \times 3 \times 2!$. Then, we simplify the 2!:
$latex\frac{{5!}}{{(2)!}}=\frac{{5\times 4\times 3\times 2!}}{{(2)!}}$
$latex =5\times 4\times 3=60$
→ Permutations Calculator (nPr)
Permutations – Practice problems
Practice and test your knowledge of permutations. Select an answer and check it to see if you chose the correct answer. If you need help, you can look at the solved examples above.
See also
Interested in learning more about factorials, permutations, and combinations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
