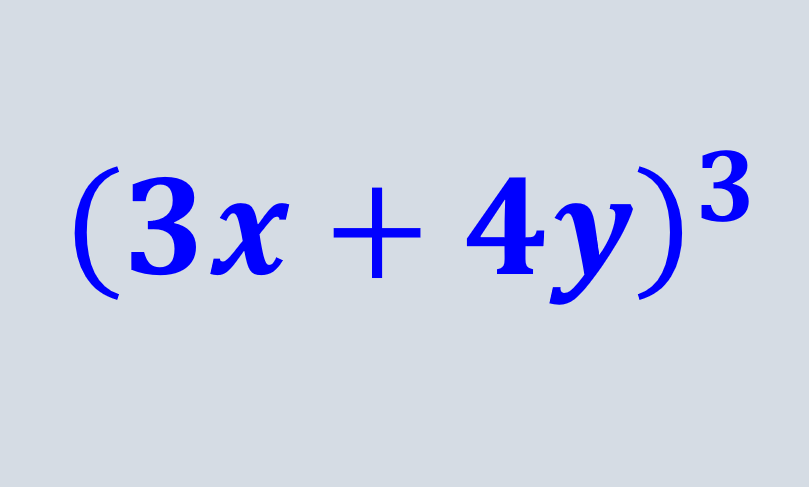Binomials cubed exercises can be solved using two methods. The first method consists in multiplying the binomial three times and fully expanding the expression. The second method is to use a standard formula that can simplify the resolution process.
Here, we will look at a summary of these two methods to solve binomials cubed. In addition, we will explore various examples with answers to fully master this topic.
Summary of binomials cubed
Recall that a binomial cubed is an expression of the form $latex {{(x+y)}^3}$. This expression could contain coefficients or other variables.
To solve binomials cubed, we can use two main methods:
Method 1: We can rewrite the binomial three times as a multiplication of binomials and eliminate the exponent. For example, we can rewrite $latex {{(x+y)}^3}$, as follows:
$latex (x+y)(x+y)(x+y)$
Then, we use the distributive property to multiply all the terms and obtain a simplified expression.
Method 2: Method 1 could be very tedious since we have to multiply each term by each term. To make it easier to solve binomials cubed, we can use standard formulas for adding cubes and subtracting cubes.
Sum of cubes: The sum of a binomial cubed is equal to the first term cubed, plus three times the square of the first term times the second term, plus three times the first term times the square of the second term, plus the cube of the second term. finished:
| $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$ |
Difference of cubes: The difference of a binomial cubed is equal to the first term cubed, minus three times the square of the first term times the second term, plus three times the first term times the square of the second term, minus the cube of the second term:
| $latex {{(a+b)}^3}={{a}^3}-3{{a}^2}b+3a{{b}^2}-{{b}^3}$ |
Binomials cubed – Examples with answers
The following binomial cubed examples can be used to learn how to apply the solving methods mentioned above. It is recommended that you try to solve the exercises yourself before looking at the solution.
EXAMPLE 1
Solve the binomial: $latex {{(x+1)}^3}$.
Solution
Method 1: We have to rewrite the binomial as a multiplication:
$latex {{(x+1)}^3}$
⇒ $latex (x+1)(x+1)(x+1)$
We start by multiplying the first two parentheses and then we multiply the remaining parentheses:
$latex (x+1)(x+1)(x+1)$
$latex =({{x}^2}+2x+1)(x+1)$
$latex ={{x}^3}+3{{x}^2}+3x+1$
Method 2: Using the formula for the sum of a binomial cubed $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$, we have:
⇒ $latex {{x}^3}+3{{x}^2}(1)+3x{{1}^2}+{{1}^3}$
$latex ={{x}^3}+3{{x}^2}+3x+1$
We see that we got the same answer using both methods. However, the first method is usually more tedious when we have more complicated binomials, so we will only use the second method to solve the next examples.
EXAMPLE 2
Find the result of the binomial cubed: $latex {{(x+5)}^3}$.
Solution
Using the formula for the sum of a binomial cubed $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$, we have:
⇒ $latex {{x}^3}+3{{x}^2}(5)+3x{{(5)}^2}+{{5}^3}$
$latex ={{x}^3}+15{{x}^2}+75x+125$
We see that with the standard formula we can more easily find the answer.
EXAMPLE 3
Solve the binomial cubed: $latex {{(2x-6)}^3}$.
Solution
In this case, we have to use the formula for subtracting a binomial from the cube $latex {{(a-b)}^3}={{a}^3}-3{{a}^2}b+3a{{b}^2}-{{b}^3}$. Therefore, we have:
⇒ $latex {{(2x)}^3}-3{{(2x)}^2}(6)+3(2x){{(6)}^2}-{{6}^3}$
$$=8{{x}^3}-3(4{{x}^2})(6)+3(2x)(36)-216$$
$latex =8{{x}^3}-72{{x}^2}+216x-216$
We could easily find the answer by using the formula.
EXAMPLE 4
Solve the binomial cubed: $latex {{(3x-2y)}^3}$.
Solution
We have to use the formula for the subtraction of a binomial cubed $latex {{(a-b)}^3}={{a}^3}-3{{a}^2}b+3a{{b}^2}-{{b}^3}$. Therefore, we have:
⇒ $${{(3x)}^3}-3{{(3x)}^2}(2y)+3(3x){{(2y)}^2}-{{(2y)}^3}$$
$$=27{{x}^3}-3(9{{x}^2})(2y)+3(3x)(4{{y}^2})-8{{y}^3}$$
$latex =27{{x}^3}-54{{x}^2}y+36x{{y}^2}-8{{y}^3}$
EXAMPLE 5
Solve the binomial cubed $latex {{(2{{x}^2}+4y)}^3}$.
Solution
Here, we have to use the formula for the sum of a binomial cubed $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$. Therefore, we have:
⇒ $${{(2{{x}^2})}^3}+3{{(2{{x}^2})}^2}(4y)+3(2{{x}^2}){{(4y)}^2}+{{(4y)}^3}$$
$$=8{{x}^6}+3(4{{x}^4})(4y)+3(2{{x}^2})(16{{y}^2})+64{{x}^3}$$
$latex =8{{x}^6}+48{{x}^4}y+96{{x}^2}{{y}^2}+64{{x}^3}$
This binomial contained a squared variable, but we apply the binomial sum formula in the same way as in the previous exercises.
We simply use the power of a power rule, which tells us that when we raise an expression with a power to another power, we have to multiply the exponents.
EXAMPLE 6
Simplify this expression: $latex {{(x+2y)}^3}+{{(x-2y)}^3}$.
Solution
We can use the formulas for adding a binomial cubed and subtracting a binomial cubed separately to calculate each binomial. Therefore, we have:
⇒ $${{(x)}^3}+3{{(x)}^2}(2y)+3(x){{(2y)}^2}+{{(2y)}^3}$$
$latex ={{x}^3}+3({{x}^2})(2y)+3(x)(4{{y}^2})+8{{y}^3}$
$latex ={{x}^3}+6{{x}^2}y+12x{{y}^2}+8{{y}^3}$
⇒ $${{(x)}^3}-3{{(x)}^2}(2y)+3(x){{(2y)}^2}-{{(2y)}^3}$$
$latex ={{x}^3}-3({{x}^2})(2y)+3(x)(4{{y}^2})-8{{y}^3}$
$latex ={{x}^3}-6{{x}^2}y+12x{{y}^2}-8{{y}^3}$
Now, we can add both expressions obtained and simplify like terms:
$$={{x}^3}+6{{x}^2}y+12x{{y}^2}+8{{y}^3}+{{x}^3}-6{{x}^2}y+12x{{y}^2}-8{{y}^3}$$
$latex =2{{x}^3}+24x{{y}^2}$
Binomials squared – Practice problems
Use the formulas for adding a binomial cubed and subtracting a binomial cubed detailed above to solve the following problems. If you have trouble with these problems, you can look at the solved examples above.
See also
Interested in learning more about factoring and the quadratic formula? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
