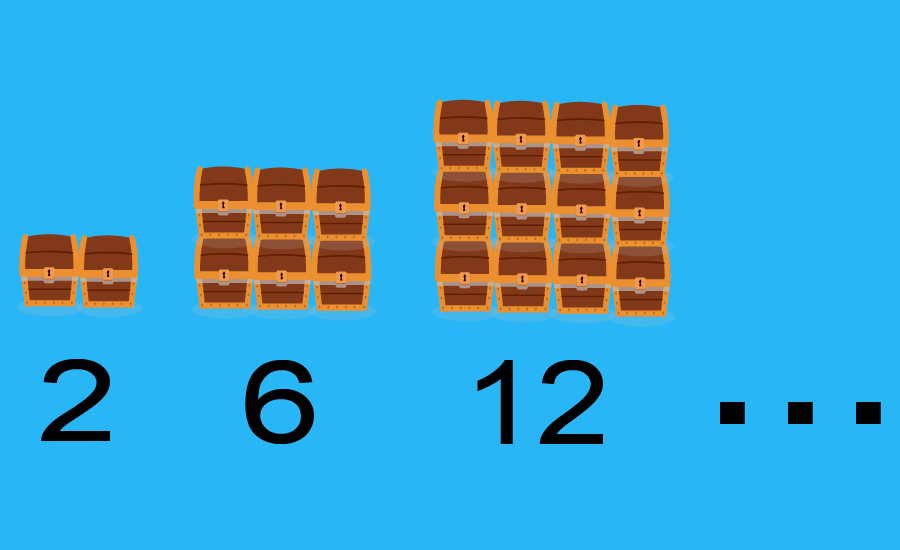Arithmetic sequences exercises can be solved using the arithmetic sequence formula. This formula allows us to find any number in the sequence if we know the common difference, the first term, and the position of the number that we want to find.
Here, we will look at a summary of arithmetic sequences. In addition, we will explore several examples with answers to understand the application of the arithmetic sequence formula.
Summary of arithmetic sequences
An arithmetic sequence is a list of numbers that has a defined pattern. We can determine if a sequence is arithmetic by taking any number and subtracting it by the previous number. Arithmetic sequences have a constant difference between consecutive numbers.
The constant difference between the consecutive numbers of an arithmetic sequence is called the common difference and denoted by the letter d. If the common difference is positive, we have an increasing arithmetic sequence and if the common difference is negative, we have a decreasing arithmetic sequence:
We can find different terms of the arithmetic sequence using the following formula:
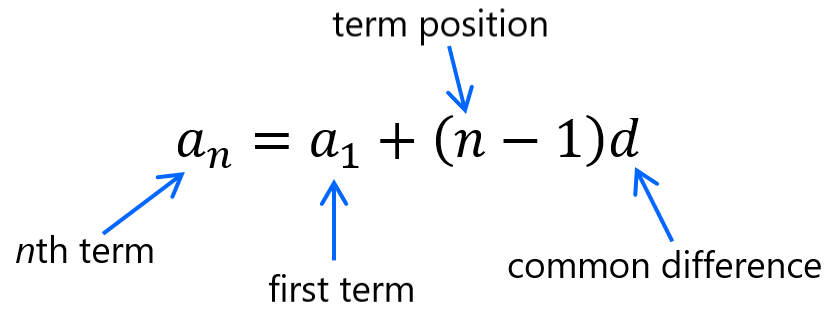
To determine any term in the arithmetic sequence, we have to know the common difference, a term in the sequence, and the position of the term that we want to determine.
Arithmetic sequences – Examples with answers
EXAMPLE 1
Find the next term in the arithmetic sequence: 3, 7, 11, 15, ?.
Solution
First, we have to find the common difference of each pair of consecutive numbers:
- $latex 15-11=4$
- $latex 11-7=4$
- $latex 7-3=4$
The common difference is 4. To find the next term after 15, we simply have to add 4 to 15. Therefore, we have $latex 15+4=19$.
EXAMPLE 2
Find the next term in the sequence: 28, 23, 18, 13, ?.
Solution
We start by finding the common difference:
- $latex 13-18=-5$
- $latex 18-23=-5$
- $latex 23-28=-5$
In this case, we obtained a negative common difference. To find the next term, we just have to add this difference to the last term. Thus, we have $latex 13+(-5)=8$.
EXAMPLE 3
Find the following two terms in the arithmetic sequence: -17, -13, -9, -5, ?, ?.
Solution
At first glance, we may think that we have a negative common difference since we have negative numbers, but we have to remember that when the sequence is growing, the common difference is positive:
- $latex -5-(-9)=4$
- $latex -9-(-13)=4$
- $latex -13-(-17)=4$
We see that the common difference is positive 4 because the arithmetic sequence is growing. We can obtain the following two terms by adding the common difference to the last term:
$latex -5+4=-1$
$latex -1+4=3$
EXAMPLE 4
In an arithmetic sequence, the first term is 8 and the common difference is 2. Find the value of the 10th term.
Solution
We begin by writing down the information given:
- First term: $latex a_{1}=8$
- Common difference: $latex d=2$
- Position of term: $latex n=10$
Now, we can use the formula for arithmetic sequences with the given information:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{10}=8+(10-1)2$
$latex a_{10}=8+(9)2$
$latex a_{10}=8+18$
$latex a_{10}=26$
EXAMPLE 5
The first term of an arithmetic sequence is 12 and the common difference is -5. What is the value of the 8th term?
Solution
We have the following values:
- First term: $latex a_{1}=12$
- Common difference: $latex d=-5$
- Position of term: $latex n=8$
Using the formula for the nth term with the given values, we have:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{8}=12+(8-1)(-5)$
$latex a_{8}=12+(7)(-5)$
$latex a_{8}=12-35$
$latex a_{8}=-23$
EXAMPLE 6
Find the 26th term in the arithmetic sequence: 3, 6, 9, 12, …
Solution
In this case, we have to use the arithmetic sequence formula $latex a_{n} = a_{1} + (n-1) d$. To use this formula, we have to know the first term, the common difference, and the position of the term we want to find:
- First term: $latex a_{1}=3$
- Common difference: $latex d=3$
- Position of term: $latex n=26$
Now, we substitute these values in the formula and solve:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{26}=3+(26-1)3$
$latex a_{26}=3+(25)3$
$latex a_{26}=3+75$
$latex a_{26}=78$
EXAMPLE 7
Find the 22nd term in the arithmetic sequence: 15, 8, 1, -6, …
Solution
We have to find the first term, the common difference and the position of the term to substitute in the arithmetic sequence formula:
- First term: $latex a_{1}=15$
- Common difference: $latex d=-7$
- Position of terms: $latex n=22$
We substitute these values in the formula:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{22}=15+(22-1)(-7)$
$latex a_{22}=15+(21)(-7)$
$latex a_{22}=15-147$
$latex a_{22}=-132$
EXAMPLE 8
Find the 16th term in the arithmetic sequence: $latex \frac{5}{2}$, 3, $latex \frac{7}{2}$, 4, …
Solution
In this case, we have fractional numbers, but similar to the previous problems, we just have to find the different values to substitute in the arithmetic sequence formula:
- First term: $latex \frac{5}{2}$
- Common difference: $latex \frac{1}{2}$
- Position of term: $latex n=16$
Now, we use the formula with these values:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{16}=\frac{5}{2}+(16-1)\frac{1}{2}$
$latex a_{16}=\frac{5}{2}+(15)\frac{1}{2}$
$latex a_{16}=\frac{5}{2}+\frac{15}{2}$
$latex a_{16}=10$
EXAMPLE 9
The 3rd term of an arithmetic sequence is equal to 10 and the 6th term is equal to 19. What is the value of the 10th term?
Solution
We know neither the value of the first term nor the common difference. However, we can find the value of the common difference considering that it is a constant value.
Then, we subtract the values of the terms and divide by the difference of their positions:
$$d=\frac{19-10}{6-3}=\frac{9}{3}=3$$
Now, we can use the formula for the nth term by considering the 6th term as the first term. Then, the 10th term is now the 5th term and the value of n is 5:
- First term: 19
- Common difference: 3
- Position of term: 5
Now, we use the formula with these values:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{4}=19+(5-1)3$
$latex a_{4}=19+(4)3$
$latex a_{4}=19+12$
$latex a_{4}=31$
This term is the 10th term of the sequence initially given.
EXAMPLE 10
Find the 14th term of an arithmetic sequence if the 4th term is 5 and the 7th term is -10.
Solution
Similar to the previous example, we find the common difference by dividing the difference in the values of the terms by the difference in their positions:
$$d=\frac{-10-5}{7-4}=\frac{-15}{3}=-5$$
Now, we consider the 7th term as the 1st term, so now the 14th term is the 8th term:
- First term: -10
- Common difference: -5
- Position of term: 6
Now, we use the formula with these values:
$latex a_{n}=a_{1}+(n-1)d$
$latex a_{6}=-10+(8-1)(-5)$
$latex a_{6}=-10+(7)(-5)$
$latex a_{6}=-10-35$
$latex a_{6}=-45$
Arithmetic sequences – Practice problems
What is the 18th term of the arithmetic sequence in which the 4th term is 17 and the 8th term is -13?
Write the answer in the input box.
See also
Interested in learning more about sequences? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
