Characteristics of Absolute Value Functions

Definition of absolute value

Let’s imagine that we are driving a car and when looking at a traffic sign, we see that the speed limit is 80 km/h. Looking at the speedometer, we see that we are traveling at 70 km/h, therefore we are traveling at 10 km / h below the speed limit.

Note that, even though we are traveling at 10 km/h below the speed limit, we are not saying that we are traveling at -10 km/h below the speed limit. We simply indicate the difference as a positive number. This is an example of absolute value in real life.

The absolute value of a number is written as |x|. The absolute value basically makes x always positive. The formal definition of the absolute value of a number is the distance between that number and zero on a number line:

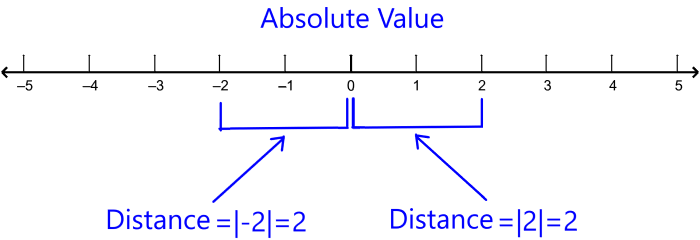
In the same way that we indicate the difference in velocity with a positive number, we indicate the distance from zero to a number on the number line with a positive number. Therefore, the absolute value of a number is the positive value of that number. For example, the absolute value of -3 is 3 and the absolute value of 3 is also 3.

---

Characteristics of absolute value functions

The following are some of the most important features of the absolute value function:

• In its most basic form, the absolute value function is f(x) = |x|.
• Its domain is all real numbers.
• Its range is all real numbers greater than or equal to zero.
• Its graph is completely above the x-axis.
• Its graph is symmetric with respect to the y axis.
• The vertex of your graph is the point (0, 0).

---

How to graph absolute value functions?

To graph an absolute value function, we have to consider that this function has a reflection with respect to the y-axis. In its basic form, $latex f(x) = | x |$, the absolute value function has a “V” shape:

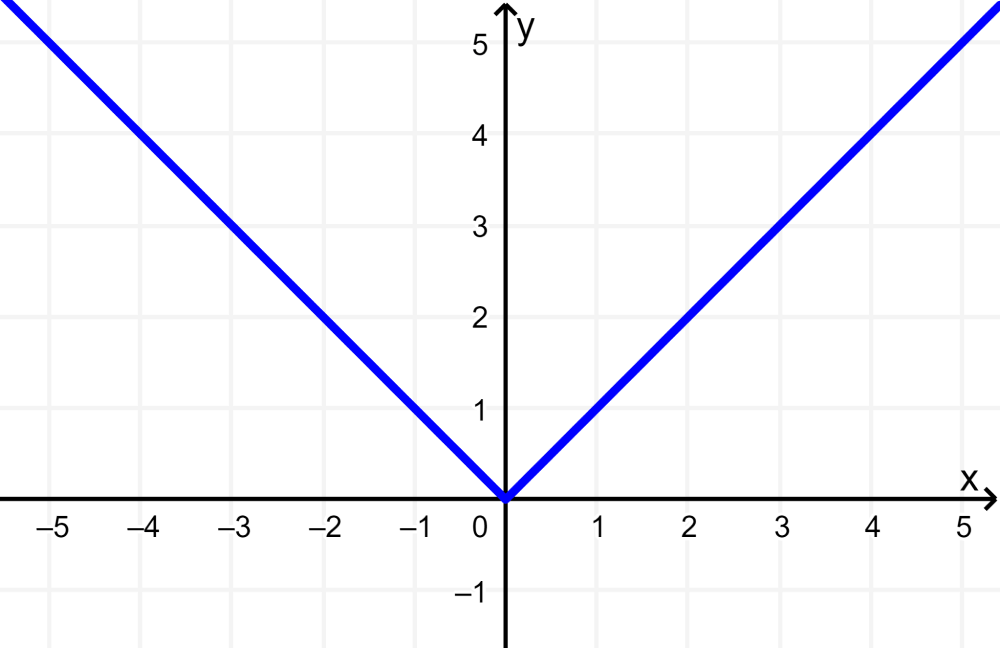
This graph satisfies the characteristics mentioned above. Its domain is all real numbers and its range is all real numbers greater than or equal to zero. Furthermore, we can see that the graph is completely above the x-axis and that it is symmetric with respect to the y-axis.

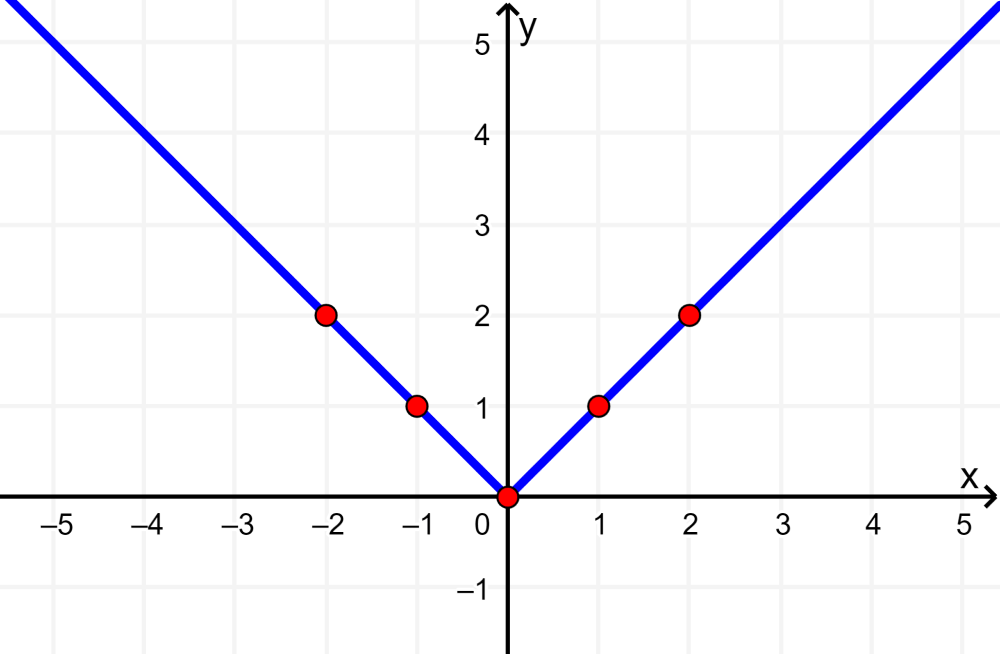
We can also graph an absolute value function by choosing multiple values for x and forming pairs of coordinates:

x	y=|x|
-2	2
-1	1
0	0
1	1
2	2

We plot the points on a Cartesian plane and connect them:

Vertical displacement

We can displace to the graph of $latex f(x)=|x|$ vertically with the function $latex g(x)=f(x)+k$.

When we have $latex k>0$, the graph is displaced k units up:

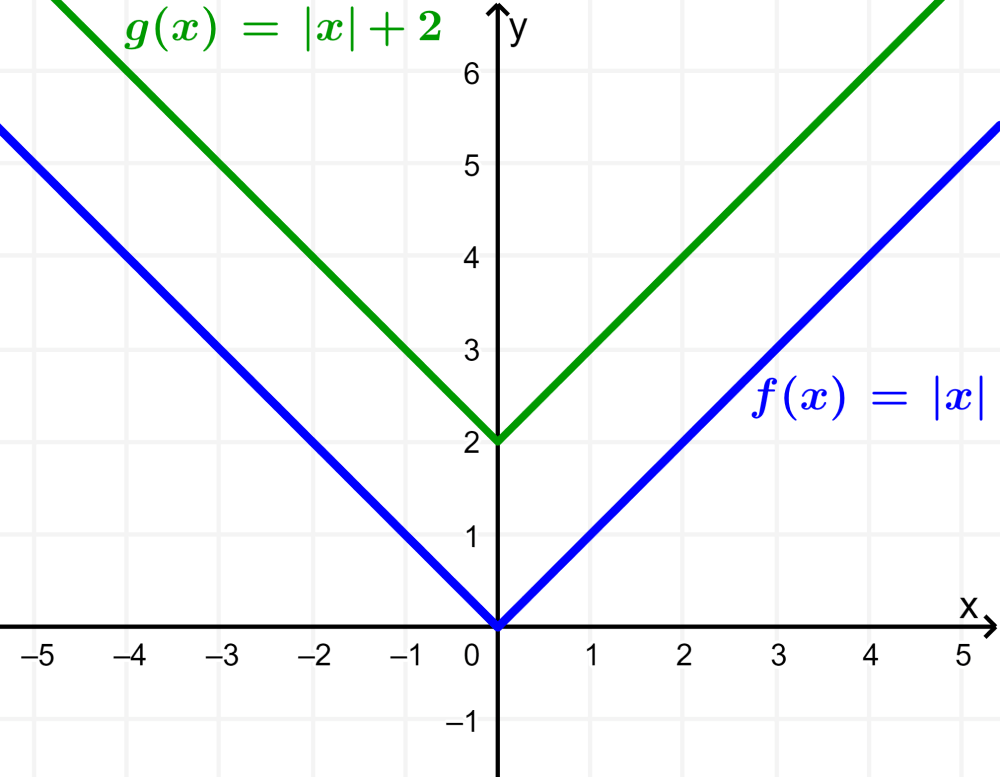
When we have $latex k<0$, the graph is displaced k units down:

Horizontal displacement

We can displace the graph of $latex f(x)=|x|$ horizontally by using the function $latex g(x)=f(x-h)$. When we have $latex h>0$, the graph is displaced h units to the right.

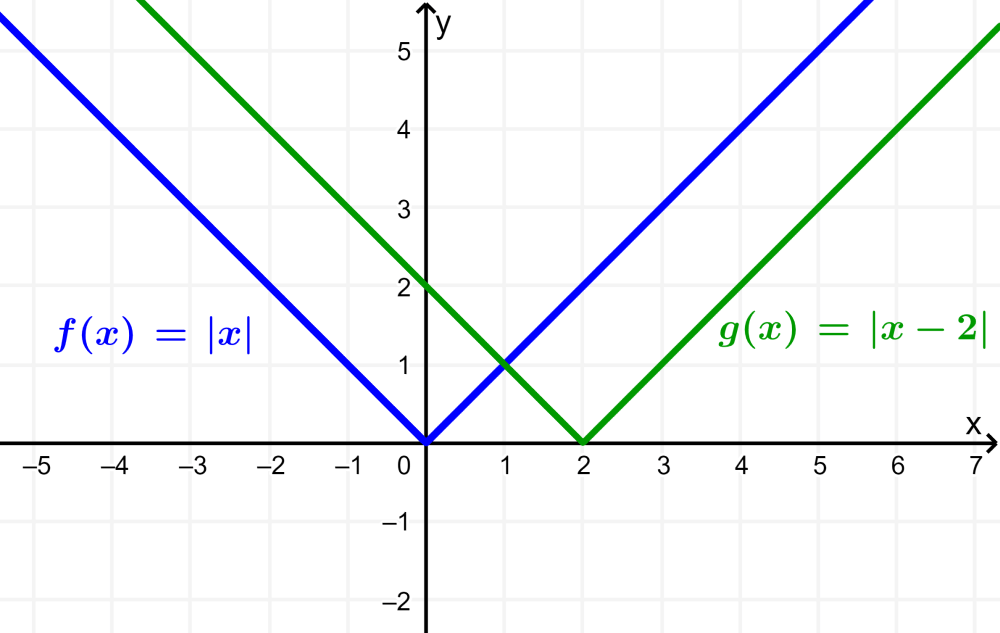
When we have $latex k<0$, the graph is displaced h units to the left.

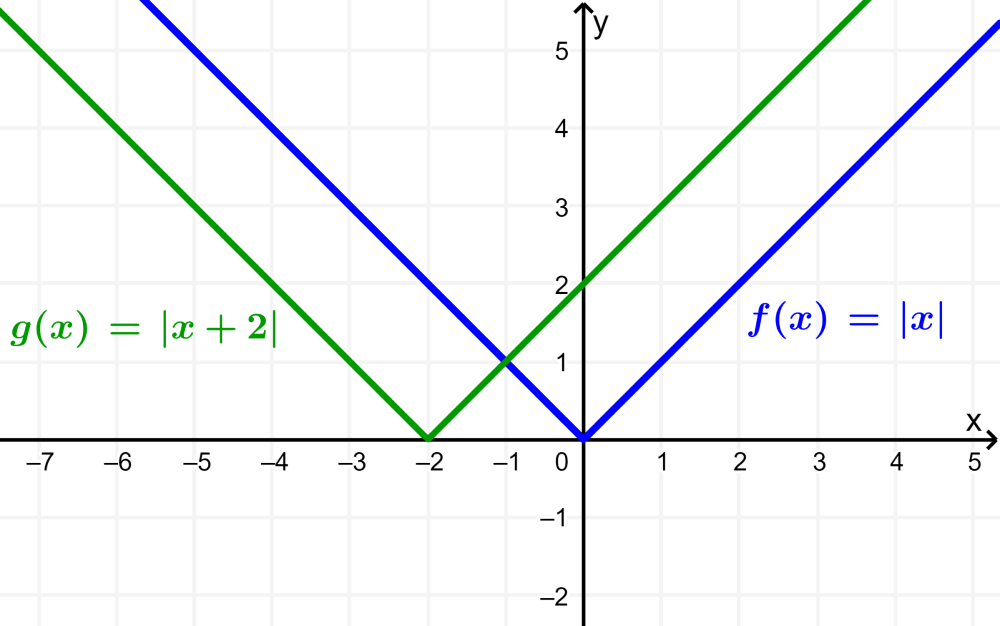
Compression and stretching

Compressing or stretching of the function $latex f(x)=|x|$ is defined by $latex f(x)=a|x|$, where a is a constant. If we have $latex a>0$, the graph opens up and if we have $latex a<0$, the graph opens down:

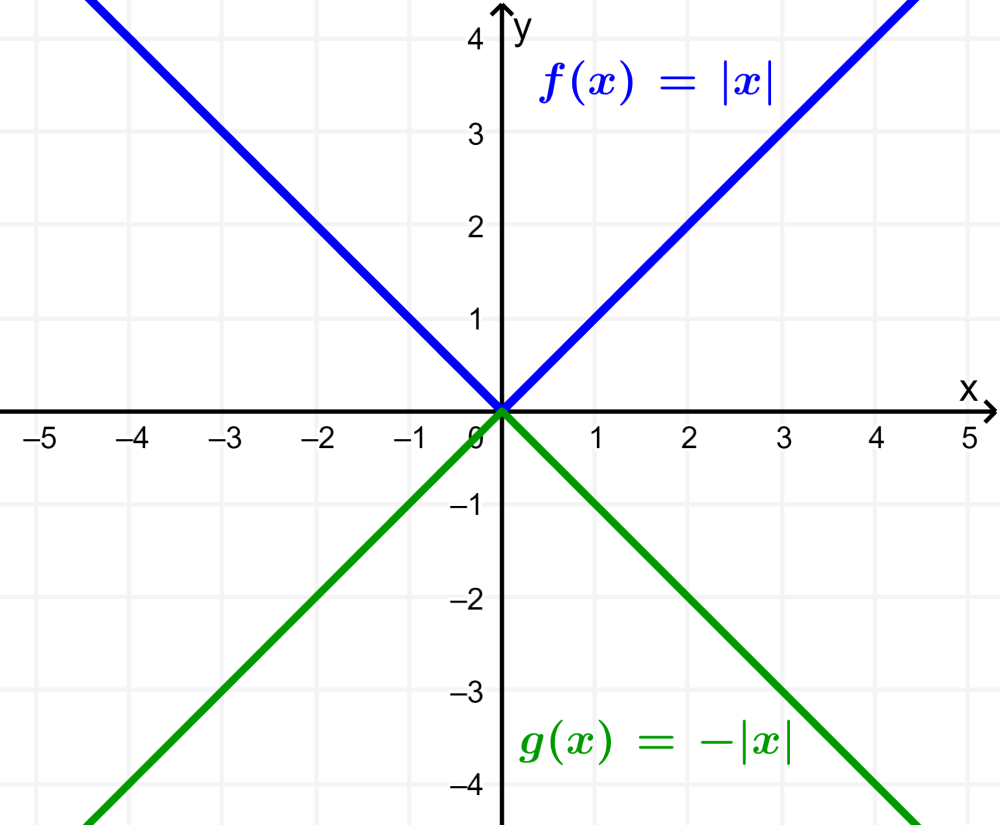
If we have $latex 1> a> 0$, the graph is compressed and if we have $latex a> 1$, the graph is stretched:

---

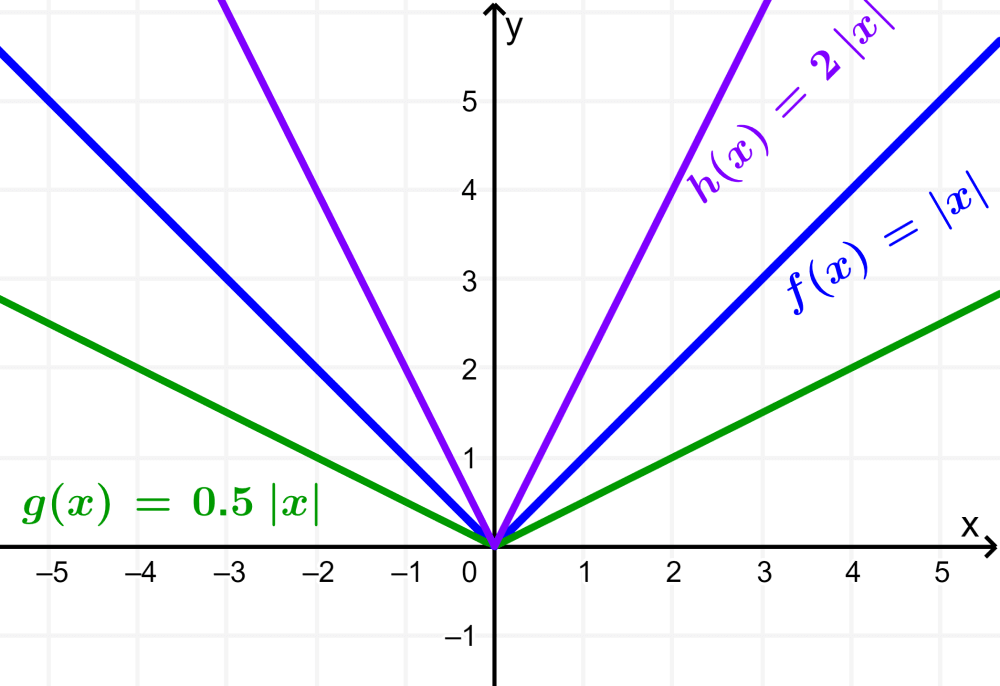
See also

Interested in learning more about absolute value? Take a look at these pages:

• Absolute Value – Definition and Applications
• Inequalities with Absolute Value