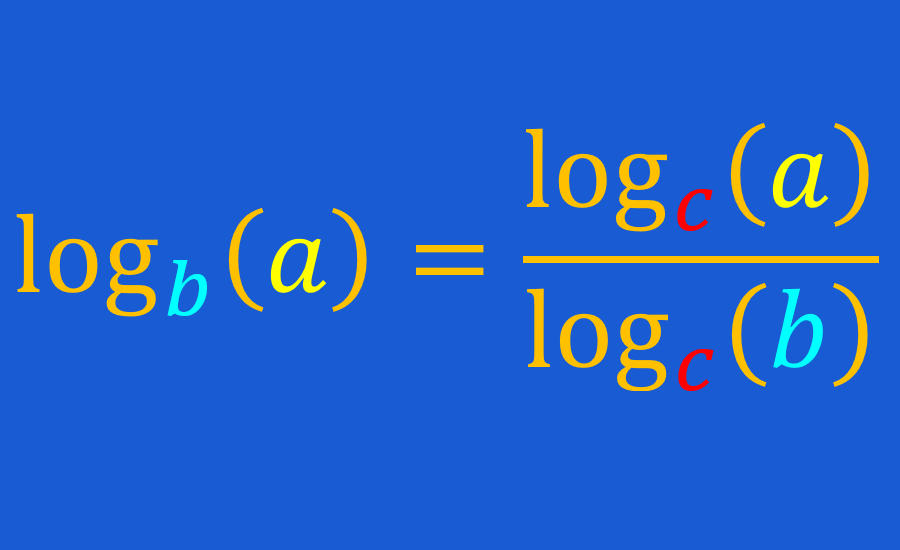The formula for change of bases of logarithms can be useful when we do not have calculators that allow us to enter logarithms of any base. Using this formula we can rewrite logarithms as a division of logarithms with the same base.
Here, we will learn about the formula for the change of bases of logarithms. In addition, we will learn to apply this formula using several examples with answers.
Change of base of logarithms formula
You may have noticed that many calculators only allow you to evaluate common logarithms (base 10) and natural logarithms (base e). We can use the change of bases formula to rewrite logarithms as the quotient of logarithms of any other base; when we use a calculator, we could change them to common or natural logarithms.
According to the logarithm base change formula, we can rewrite any logarithm as the quotient of two logarithms with a new base:
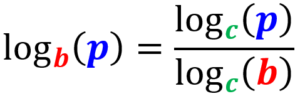
Proof of the change of bases formula
We can check that the formula for change of bases is true by starting with the logarithm $latex x=\log_{b}(p)$. We know that logarithms and exponentials are inverse functions, so we can write the logarithm in its exponential form:
⇒ $latex {{b}^x}=p$
Now, we can take a logarithm with base “c” on both sides of the expression and we have:
$latex \log_{c}({{b}^{x}})=\log_{c}(p)$
We can use the logarithm of a power rule, which tells us that we can rewrite as follows:
$latex (x)\log_{c}(b)=\log_{c}(p)$
We can divide both sides by $latex \log_{c}(b)$ to solve for x:
$latex x=\frac{\log_{c}(p)}{\log_{c}(b)}$
Now, we substitute the original value of x, $latex x=\log_{b}(p)$:
| $latex \log_{b}(p)=\frac{\log_{c}(p)}{\log_{c}(b)}$ |
In practical terms, this formula tells us that we can evaluate a logarithm with a non-standard base by converting it to a fraction of the form “(logarithm with a standard base of argument) divided by (log with the same base of non-standard base ) “.
Change of base of logarithms – Examples with answers
The following examples are solved using the formula for the change of logarithm bases. Each example has its respective solution, but it is recommended that you try to solve the examples yourself before looking at the answer.
EXAMPLE 1
Write $latex \log_{3}(7)$ as a quotient of natural logarithms.
Solution
Since we are going to express the logarithm as a quotient of natural logarithms, the new base is e.
We rewrite the logarithm as a quotient of natural logarithms using the change of bases formula. The numerator of the quotient will be the natural logarithm with argument 7. The denominator of the quotient will be the natural logarithm with argument 3:
$latex \log_{3}(7)=\frac{\log_{e}(7)}{\log_{e}(3)}$
$latex =\frac{\ln(7)}{\ln(3)}$
EXAMPLE 2
Evaluate $latex \log_{2}(10)$ using the change of bases formula with a calculator.
Solution
According to the formula for the change of bases, we can write the logarithm base 2 as a logarithm of any other base. Since calculators do contain the natural logarithm, we can use the natural logarithm:
$latex \log_{2}(10)=\frac{\ln(10)}{\ln(2)}$
$latex \approx 3.3219$
EXAMPLE 3
Convert $latex \log_{2}(7)$ to a logarithm with base 5.
Solution
Although transforming to a logarithm with base 5 would not be very useful for problem-solving, these exercises are intended to practice using the change of bases formula. Therefore, we have:
$latex \log_{2}(7)=\frac{\log_{5}(7)}{\log_{5}(2)}$
EXAMPLE 4
Evaluate the logarithm $latex \log_{3}(6)$.
Solution
The argument is 6 and a base is 3. We can use the formula for change of bases and change to a quotient of natural logarithms:
$latex \log_{3}(6)=\frac{\ln(6)}{\ln(3)}$
$latex =\frac{1.7916}{1.6309}$
If we round to three decimal places, the final answer is:
$latex \log_{3}(6)=1.631$
We could also use the common logarithm:
$latex \log_{3}(6)=\frac{\log(6)}{\log(3)}$
$latex =\frac{0.7782}{0.4771}$
$latex =1.631$
We can see that it does not matter which base we use in the formula for the change of bases. The only important thing is that we keep the same base in both the numerator and the denominator.
EXAMPLE 5
Simplify the expression $latex \frac{\log(625)}{\log(25)}$ to get a single real number.
Solution
In this case, we can use the reverse base change formula, that is, we start with the quotient and obtain the following logarithm:
$latex \frac{\log(625)}{\log(25)}=\log_{25}(625)$
Now, we can rewrite this logarithm as a power to make solving easier. We say that the result of this logarithm is given by the letter x:
$latex {{25}^x}=625$
We can rewrite this as powers with the same base:
$latex {{({{5}^2})}^x}={{5}^4}$
$latex {{5}^{2x}}={{5}^4}$
Since the bases are equivalent, it means that the exponents must also be equivalent for the equation to be true. Therefore, we have:
$latex 2x=4$
$latex x=2$
Therefore, the value of the original expression is 2.
Change of base of logarithms – Practice problems
Practice what you have learned about the change of bases formula with the following problems. Solve the problems and select your answer. Please check it to make sure you selected the correct one.
See also
Interested in learning more about natural logarithms? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
