Pascal’s triangle has many applications in mathematics and statistics. We can use Pascal’s triangle to find the binomial expansion. Also, Pascal’s triangle is used in probabilistic applications and in the calculation of combinations. Recall that Pascal’s triangle is a pattern of numbers in the shape of a triangle, where each number is found by adding the two numbers above it.
Here, we will look at each of the most important applications of Pascal’s triangle in detail along with some examples to understand their use.
ALGEBRA
Relevant for…
Learning about some of the applications of Pascal’s triangle.
ALGEBRA
Relevant for…
Learning about some of the applications of Pascal’s triangle.
Pascal’s triangle in binomial expansion
The following is Pascal’s triangle:
We can use the rows of Pascal’s triangle to facilitate the binomial expansion process. Depending on the power of a binomial, we can use a given row of Pascal’s triangle that represents the coefficients of the expanded values.
We use $latex n + 1$ to determine the row to use, where n represents the power of the binomial. Alternatively, we can consider the first row as 0 and take the row in Pascal’s triangle indicated by the power. For example, let’s look at the following binomial expansion:
$latex {{(a+b)}^2}=1{{a}^2}+2ab+1{{b}^2}$
In this expansion, we have the coefficients 1, 2, 1. This corresponds to the third row of Pascal’s triangle. We see that the power of the binomial is 2, so when using $latex n + 1$, we have 3 that does correspond to the third row used.
EXAMPLE
- Expand the binomial $latex {{(x+y)}^4}$.
Solution: In this case, the power is 4, so we have to use the row number $latex 4 + 1 = 5$. This row corresponds to the numbers 1, 4, 6, 4, 1. These are the coefficients of the binomial expansion and it tells us that we will have 5 terms in the expansion.
Furthermore, we know that we expand a binomial by starting with each term in the highest power and reducing to 0 each term in the opposite direction:
$latex {{(x+y)}^4}$
$$=1{{x}^4}{{y}^0}+4{{x}^3}{{y}^1}+6{{x}^2}{{y}^2}+4{{x}^1}{{y}^3}+1{{x}^0}{{y}^4}$$
$$=1{{x}^4}(1)+4{{x}^3}{{y}^1}+6{{x}^2}{{y}^2}+4{{x}^1}{{y}^3}+1(1){{y}^4}$$
$$={{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}$$
Pascal’s triangle in probability
Pascal’s triangle can be used in probability to simplify counting the probabilities of some event. For example, Pascal’s triangle can show us in how many ways we can combine heads and tails in a coin toss.
Then, this can show us the probability of any combination. In the following example, T represents tails and H represents heads.
EXAMPLE
Suppose a coin is tossed 4 times, the probabilities of the combinations are:
- HHHH
- HHHT, HHTH, HTHH, THHH
- HHTT, HTHT, HTTH, THHT, THTH, TTHH
- HTTT, THTT, TTHT, TTTH
- TTTT
Therefore, the observed pattern is 1, 4, 6, 4, 1. If we are looking for the total number of possibilities, we just have to add the numbers. That is, we have $latex 1 + 4 + 6 + 4 + 1 = 16$ possible combinations if we toss a coin 4 times.
Pascal’s triangle in combinations
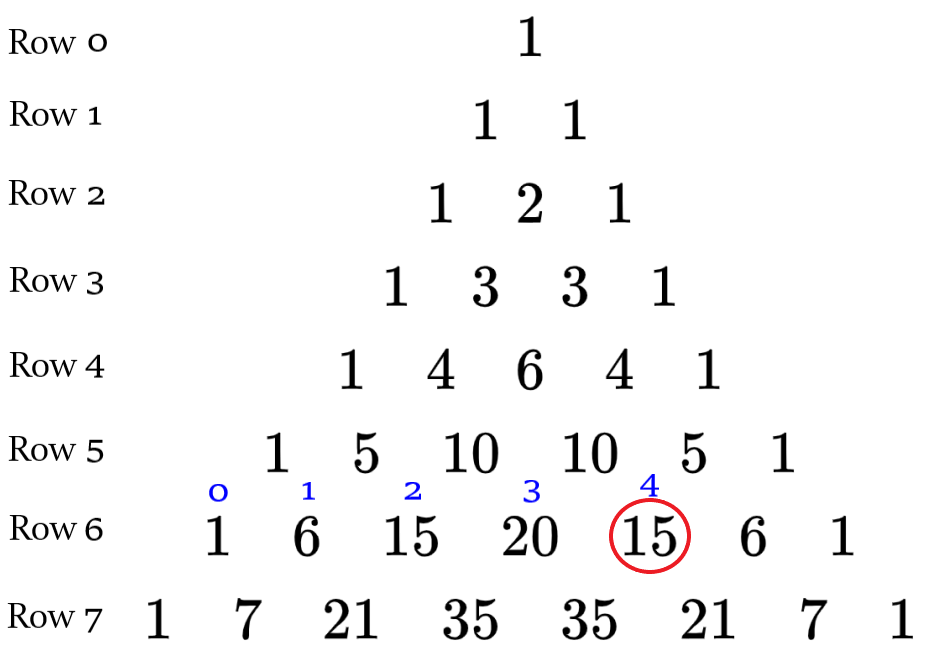
Pascal’s triangle can be used to find combinations. The top row of Pascal’s triangle is row 0, and the first number in each row is element zero of that row. For example, if we want to find the combination $latex _{6} C _{4}$, we have to look at row 6 and item 4. The answer is 15:
EXAMPLE
- We have 5 marbles in a bag, 1 red, 1 blue, 1 green, 1 yellow, and 1 black. How many combinations are possible if we want to choose 2 marbles?
Solutions: The total number of marbles is 5 and we want to choose 2 marbles. Therefore, we have the combination $latex _{5} C _{2}$. This means that we have to look at element 2 in row 5. This means that the answer is 10.
See also
Interested in learning more about Pascal’s triangle and the binomial theorem? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
