Spherical Coordinates – Formulas and Diagrams

What are spherical coordinates?

Spherical coordinates are a three-dimensional coordinate system. This system has the form (ρ, θ, φ), where ρ is the distance from the origin to the point, θ is the angle formed with respect to the x-axis and φ is the angle formed with respect to the z-axis.

The spherical coordinate system is useful when we want to graph spherical figures or figures that are defined using different angles. This coordinate system is mainly convenient in Calculus.

Many times, finding the derivatives or integrals of spherical figures can be easier using this system since we can describe the figures using simpler and more convenient equations.

---

Examples of spherical coordinates

To graph a point that is represented in spherical coordinates, we can start by locating it with respect to its distance from the origin and its angle with respect to the x-axis. Then, we locate it with respect to the angle it makes from the z-axis. The diagram below represents the point $latex (3, \frac{\pi}{3}, \frac{\pi}{4})$.

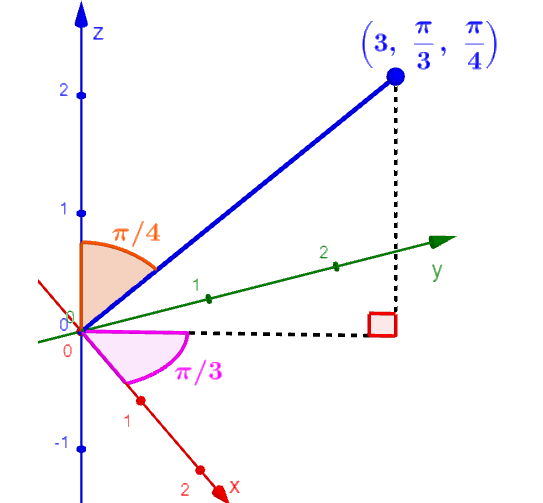
We can see that the angle φ is measured from the positive z-axis. This angle goes from 0 to π. On the other hand, the angle θ has no restriction. This means that we actually have several ways of representing a point in spherical coordinates.

This is because, if we add or subtract 2π or a multiple of 2π, we get an equivalent angle. For example, the angles $latex \frac{\pi}{3}, \frac{4 \pi}{3}, \frac{2 \pi}{3}$ are equivalent.

---

Spherical to Cartesian conversion formulas

Let’s use the following diagram to derive the formulas for converting spherical coordinates to Cartesian coordinates:

We can use right triangles and trigonometry to obtain equations for ρ, θ, φ in terms of x, y, z. The derivation of these equations is easier if we start transforming from spherical to cylindrical coordinates and then from cylindrical to Cartesian coordinates. Therefore, we use the following diagram:

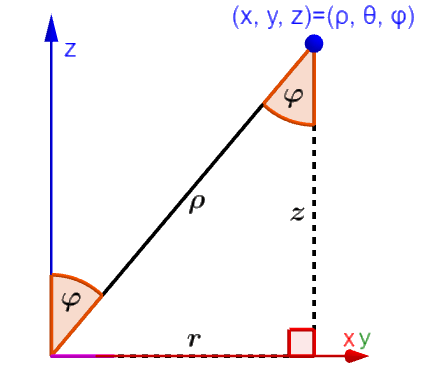
We can find r and z using the sine and cosine functions respectively:

$latex z=\rho \cos(\phi)$

$latex r=\rho \sin(\phi)$

The third component here is $latex \theta$. Now, we use the transformation formulas from cylindrical to Cartesian coordinates:

$latex x=r~\cos(\theta)$

$latex y=r~\sin(\theta)$

$latex z=z~~~~~$

If we use these two sets of equations, we have:

$latex x=\rho \sin(\phi)\cos(\theta)$ $latex y=\rho \sin(\phi)\sin(\theta)$ $latex z=\rho \cos(\phi)~~$

---

Cartesian to spherical conversion Formulas

To derive the conversion formulas from Cartesian coordinates to spherical coordinates, we use the same diagram:

The component ρ can be found in terms of x, y, z using the Pythagorean theorem in three dimensions. Therefore, we have:

$latex {{\rho}^2}={{x}^2}+{{y}^2}+{{z}^2}$

$latex \rho=\sqrt{{{x}^2}+{{y}^2}+{{z}^2}}$

The angle θ is found using the same cylindrical coordinate process. We use the inverse tangent, where, y is the opposite side of the angle and x is the adjacent side. Therefore, we have:

$latex \theta=\tan^{-1}(\frac{y}{x})$

Something that we must consider is that, many times the angle given by the calculator is not correct. This is because the inverse tangent function has a range from $latex – \frac{\pi}{2}$ to $latex \frac{\pi}{2}$, so it does not cover all four quadrants.

To correct this, we add 180° or π if the point is in the second or third quadrant and we add 360° or 2π if the point is in the fourth quadrant. If the point is in the first quadrant, the value given by the calculator is correct.

To find the angle φ, we can use the cosine function. We see that the side adjacent to this angle is the side z and the hypotenuse is equal to ρ. Thus, we have:

$latex \phi={{\cos}^{-1}}(\frac{z}{\rho})$

---

See also

Interested in learning more about spherical coordinates? Take a look at these pages:

• Spherical to Cartesian coordinates – Formulas and Examples
• Cartesian to Spherical Coordinates – Formulas and Examples