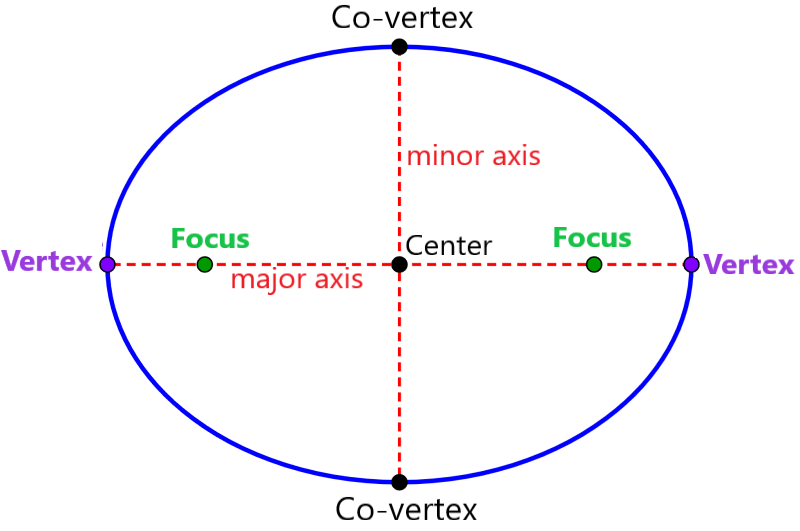
Ellipses are formed by the set of all points, which have distances from two fixed points that when added are equal to a constant value. The fixed points are called the foci of the ellipse. Ellipses have two lines of symmetries. The axis with the longest length is called the major axis and the axis with the shortest length is called the minor axis. The vertices of the ellipse are the endpoints of the major axis and the co-vertices are the endpoints of the minor axis. The center of an ellipse is the point of intersection of the major axis and the minor axis. The foci are always located on the major axis.
Here, we will learn about the equation of the ellipse that has a center outside the origin. We will look at equations for both vertically oriented ellipses and horizontally oriented ellipses.
PRECALCULUS
Relevant for…
Finding the equation of the ellipse with center outside the origin.
PRECALCULUS
Relevant for…
Finding the equation of the ellipse with center outside the origin.
Standard form of ellipses with center outside the origin
Many times, ellipses are not centered at the origin, so we cannot use the more basic equations that we use when we do have a center at the origin. However, similar to other graphs, ellipse graphs can be translated horizontally and vertically.
If an ellipse is translated h units horizontally and k units vertically, its center will be at (h, k). We can use this translation in the standard equation of an ellipse by substituting x with $latex (x-h)$ and y with $latex (y-k)$.
In addition to having ellipses centered at the origin and outside the origin, we also have ellipses that have a vertical or horizontal orientation.
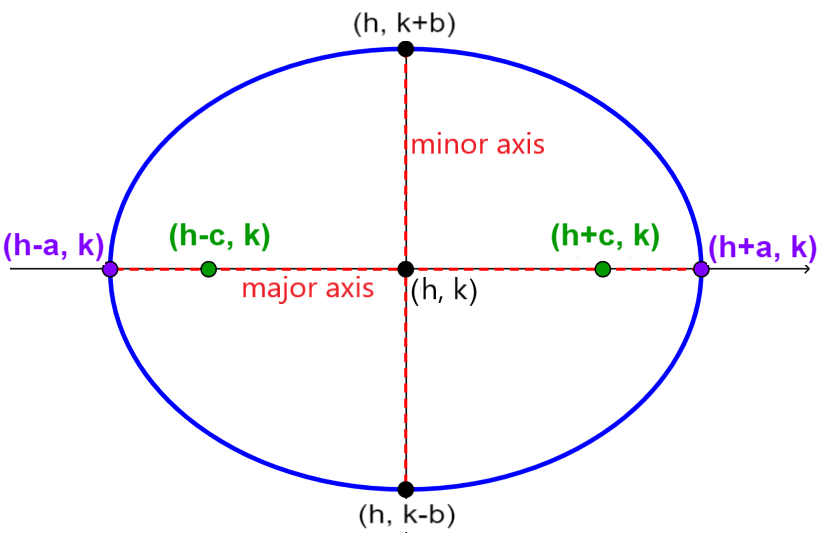
Equation of the horizontal ellipse centered outside the origin
The standard form of an ellipse centered at (h, k), and with the major axis parallel to the x axis is:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-h)}^2}}{{{b}^2}}=1$ |
where,
- $latex a>b$
- The major axis measures $latex 2a$
- The minor axis measures $latex 2b$
- The vertices are located at $latex (h\pm a, k)$
- The covertices are located at $latex (h, k\pm b)$
- The foci are located at $latex (h \pm c, k)$, where, $latex {{c}^2}={{a}^2}-{{b}^2}$
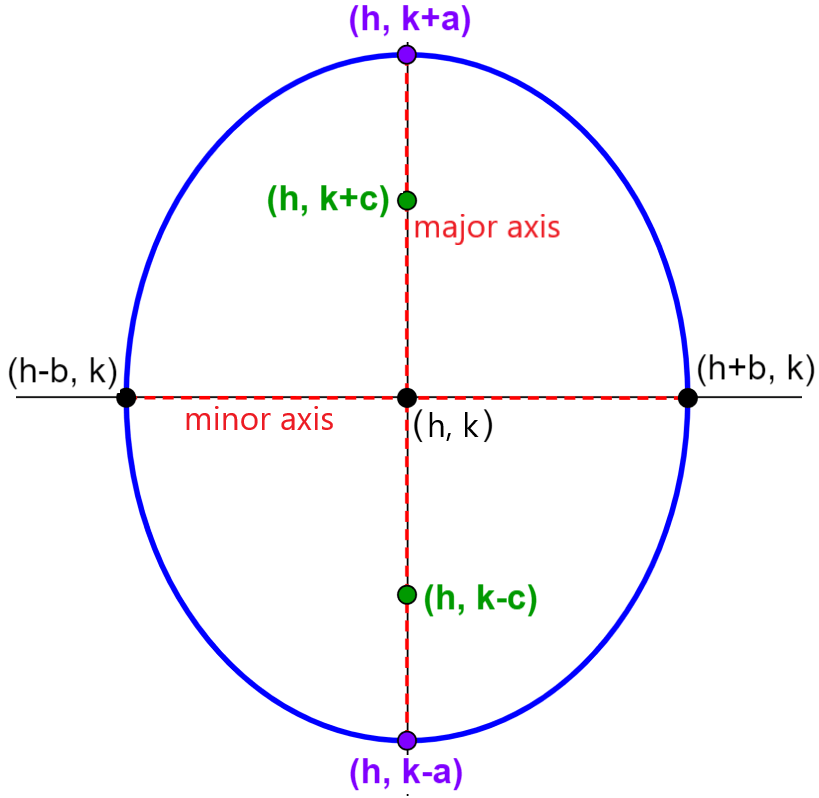
Equation of the vertical ellipse centered outside the origin
The equation of an ellipse in its standard form that has its center at (h, k), and whose major axis is parallel to the y axis is:
| $latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$ |
where,
- $latex a>b$
- The length of the major axis is $latex 2a$
- The length of the minor axis is $latex 2b$
- The vertices are located at $latex (h, k\pm a)$
- The covertices are located at $latex (h\pm b, k)$
- The foci are located at $latex (h, k\pm c)$, where, $latex {{c}^2}={{a}^2}-{{b}^2}$
Writing the equation for ellipses with center outside the origin using vertices and foci
We use the following steps to determine the equation of an ellipse centered outside the origin if we know the vertices and foci:
Step 1: Determine if the major axis is parallel to the x-axis or to the y axis.
1.1. If the y coordinates of the vertices are equal to the y coordinates of the foci, the major axis is parallel to the x-axis and we use the equation $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$.
1.2. If the x coordinates of the vertices are equal to the y coordinates of the foci, the major axis is parallel to the y axis and we use the equation $latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$.
Step 2: We can determine the coordinates of the center of the ellipse (h, k) using the coordinates of the vertices and recognizing that the center is at the midpoint.
Step 3: We find the value of $latex {{a}^2}$ by finding the length of the major axis, 2a. This length is the distance between the two vertices.
Step 4: We find the value of $latex {{c}^2}$ using the values of h and k along with the coordinates of the foci.
Step 5: We solve $latex {{b}^2}$ using the equation $latex {{c}^2}={{a}^2}-{{b}^2}$.
Step 6: We substitute the values of $latex {{a}^2}$, $latex {{b}^2}$, h and k into the equation obtained in step 1.
Ellipse with center outside the origin – Examples with answers
What has been learned about the equations of ellipses that have the center at the point (h, k) is applied to solve the following examples. Analyze the process used carefully.
EXAMPLE 1
Find the equation of the ellipse that has vertices at (-1, -9) and (-1, 3) and foci at (-1, -8) and (-1, 2).
Solution
We see that the x coordinates of the vertices and the foci are the same, so the major axis is parallel to the y axis. Therefore, the equation of the ellipse will have the following form:
$latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$
To find the center, we use the midpoint formula since the center is between the vertices $latex (-1, -9)$ and $latex (-1, 3)$. Therefore, we have:
$latex (h, k)=(\frac{-1+(-1)}{2}, \frac{-9+3}{2})$
$latex =(-1, -3)$
Now, we are going to find $latex {{a}^2}$. The length of the major axis, $latex 2a$, is limited by the two vertices. So the distance between the vertices is:
$latex 2a=3-(-9)$
$latex 2a=12$
$latex a=6$
Therefore, we have $latex {{a}^2}=36$.
Now, we find $latex {{c}^2}$. For vertical ellipses, the foci are given by $latex (h, k \pm c)$. Therefore, we have $latex (h, k-c)=(-1,-8)$ and $latex (h, k+c)=(-1,2)$. We use the value $latex k = -3$ at any of these points and solve:
$latex k+c=2$
$latex -3+c=2$
$latex c=5$
Therefore, we have $latex {{c}^2}=25$.
Now, we use the equation $latex {{c}^2}={{a}^2}-{{b}^2}$ to get the value of $latex {{b}^2}$. Therefore, we have:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 25=36-{{b}^2}$
$latex {{b}^2}=11$
Finally, we use the values obtained in the equation of the ellipse:
$latex \frac{{{(x+1)}^2}}{11}+\frac{{{(y+3)}^2}}{36}=1$
EXAMPLE 2
What is the equation of the ellipse that has vertices at (-4, 2), (8, 2) and foci at (-2, 2), (6, 2)?
Solution
In this case, the y coordinates of the vertices and foci are the same. This means that the major axis is parallel to the x-axis. Therefore, the equation of the ellipse will have the following form:
$latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$
We find the center using the midpoint formula since the center is between the vertices $latex (-4, 2)$ and $latex (8, 2)$. Therefore, we have:
$latex (h, k)=(\frac{-4+8}{2}, \frac{2+2}{2})$
$latex =(2, 2)$
We find $latex {{a}^2}$ using the length of the major axis, $latex 2a$. This length is equal to the distance between the vertices. Therefore, we have :
$latex 2a=8-(4)$
$latex 2a=12$
$latex a=6$
Therefore, we have $latex {{a}^2}=36$.
Now, we find $latex {{c}^2}$. In a horizontal ellipse, the foci are given by $latex (h \pm c, k)$. Therefore, we have $latex (h-c, k)=(-2, 2)$ and $latex (h+c, k)=(6,2)$. We use any of these points with the value $latex h=2$ and we solve:
$latex h+c=6$
$latex 2+c=6$
$latex c=4$
Therefore, we have $latex {{c}^2}=16$.
We find the value of $latex {{b}^2}$ using the equation $latex {{c}^2}={{a}^2}-{{b}^2}$. Therefore, we have:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 16=36-{{b}^2}$
$latex {{b}^2}=20$
Finally, we use the values obtained in the equation of the ellipse:
$latex \frac{{{(x-2)}^2}}{36}+\frac{{{(y-2)}^2}}{20}=1$
Ellipse with center outside the origin – Practice problems
Use what you have learned about equations for ellipses with centers outside the origin to solve the following problems. Look at the solved exercises above in case you need help with this.
See also
Interested in learning more about equations of an ellipse? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
