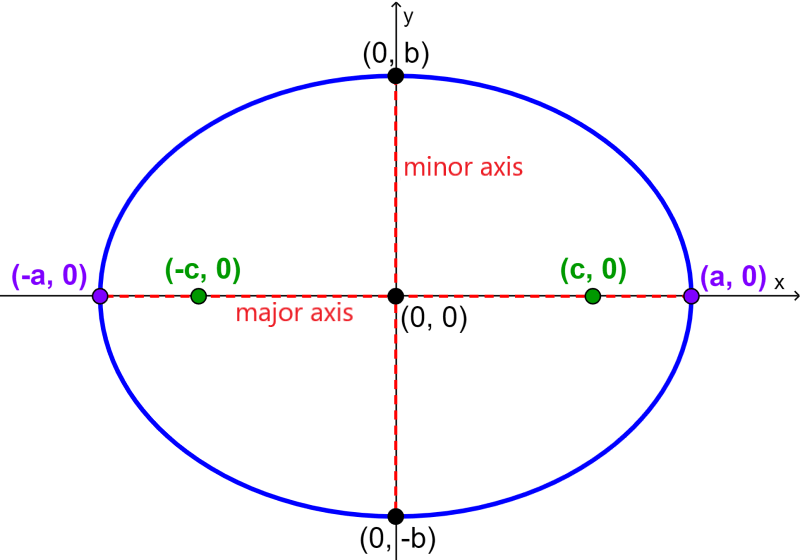
The eccentricity of the ellipse is a unique characteristic that determines the shape of the ellipse. Eccentricity means the deviation of the curve that has occurred from the circularity of a given figure. For instance, an eccentricity of 0 means that the figure is completely round, and an eccentricity less than 1 means that the figure is an oval. The eccentricity depends on the distance from the center to the foci and the distance from the center to the vertex.
Here, we will learn about the formula used to calculate the eccentricity of ellipses. We will solve some practice problems.
PRECALCULUS
Relevant for…
Learning about the eccentricity of the ellipse with examples.
PRECALCULUS
Relevant for…
Learning about the eccentricity of the ellipse with examples.
How to calculate the eccentricity of ellipses?
The eccentricity of the ellipses is calculated using the following formula:
$latex e=\frac{c}{a}$
where c represents the distance from the center to the foci and a represents the length of the semi-major axis, that is, the distance from the center to the vertex.
We can calculate the distance from the center to the foci using the formula:
$latex {{c}^2}={{a}^2}-{{b}^2}$
where a is the length of the semi-major axis and b is the length of the semi-minor axis.
We know that the foci of the ellipse are closer to the center compared to the vertices. This means that the value of the eccentricity of an ellipse will always be less than 1 since the value of the numerator will always be less than the value of the denominator.
The closer the foci get to the center, the value of the eccentricity decreases, and when the foci are in the center, the eccentricity is equal to 0 and the figure is round. That is, when we have $latex e = 0$, we no longer have an ellipse but a circle. Therefore, for an ellipse, we have:
$latex e=\frac{c}{a}$, where $latex 0<e<1$
Eccentricity of an ellipse – Examples with answers
The following ellipse eccentricity examples can be used to look at the application of the formulas seen above. Try to solve the problems yourself before looking at the answer.
EXAMPLE 1
What is the eccentricity of an ellipse that has the equation $latex \frac{{{x}^2}}{64}+\frac{{{y}^2}}{16}=1$?
Solution
From the equation, we can identify the following values:
$latex {{a}^2}=64$
$latex a=8$
$latex {{b}^2}=16$
$latex b=4$
Now, we use these values to find c with the following equation:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=64-16$
$latex {{c}^2}=48$
$latex c=6.93$
We substitute the values found in the eccentricity equation:
$latex e=\frac{c}{a}$
$latex e=\frac{6.93}{8}$
$latex e=0.87$
EXAMPLE 2
If an ellipse that has the equation $latex \frac{{{x}^2}}{81}+\frac{{{y}^2}}{25}=1$, what is its eccentricity?
Solution
We start by identifying the values of a and b of the given equation:
$latex {{a}^2}=81$
$latex a=9$
$latex {{b}^2}=25$
$latex b=5$
We find the value of c using the following equation:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=81-25$
$latex {{c}^2}=56$
$latex c=7.48$
Using the eccentricity formula with the found values, we have:
$latex e=\frac{c}{a}$
$latex e=\frac{7.48}{9}$
$latex e=0.83$
EXAMPLE 3
What is the eccentricity of an ellipse that has the equation $latex \frac{{{x}^2}}{121}+\frac{{{y}^2}}{64}=1$?
Solution
We can extract the following values from the given equation:
$latex {{a}^2}=121$
$latex a=11$
$latex {{b}^2}=64$
$latex b=8$
Using these values, we can find c with the following equation:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=121-64$
$latex {{c}^2}=57$
$latex c=7.55$
We find the eccentricity using the found values:
$latex e=\frac{c}{a}$
$latex e=\frac{7.55}{11}$
$latex e=0.69$
EXAMPLE 4
We have an ellipse with the equation $latex \frac{{{x}^2}}{144}+\frac{{{y}^2}}{121}=1$. What is its eccentricity?
Solution
We have the following values:
$latex {{a}^2}=144$
$latex a=12$
$latex {{b}^2}=121$
$latex b=11$
We find the value of c using these values in the following equation:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=144-121$
$latex {{c}^2}=23$
$latex c=4.8$
Using these data in the eccentricity equation, we have:
$latex e=\frac{c}{a}$
$latex e=\frac{4.8}{11}$
$latex e=0.44$
Eccentricity of an ellipse – Practice problems
Use what you have learned about the eccentricity of ellipses to solve the following problems. Select an answer and check it to see if you got the correct answer.
See also
Interested in learning more about ellipses? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
