Parabolas are conic sections that are obtained at the intersection of a plane with a cone. The plane has to cut the base of the cone in order for the parabola to be formed. The main characteristic of parabolas is that all the points on their curve are located at the same distance from a fixed point and from a straight line. The fixed point is the focus and the straight line is the directrix.
Here, we will look at a more detailed definition of parabolas along with a diagram to illustrate it. Then, we will learn about the most important characteristics of these conic sections.
PRECALCULUS
Relevant for…
Learning about the most important characteristics of parabolas.
PRECALCULUS
Relevant for…
Learning about the most important characteristics of parabolas.
Definition of a parabola
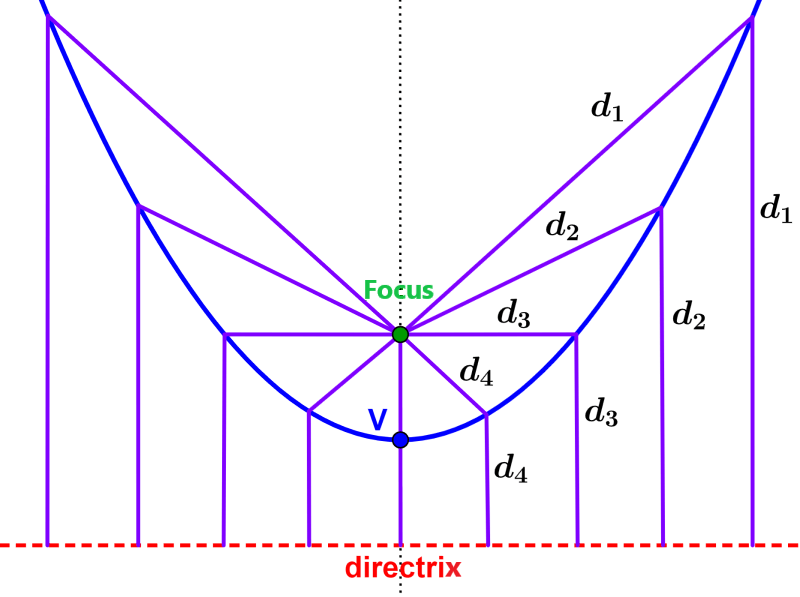
A parabola is defined as the set of points that have the same distance from a fixed point, called the focus, and a straight line called the directrix. In the following image, we have a parabola along with its focus and its directrix. We can see that each point on the parabola has the same distance from the focus and directrix.
Parabolas are also defined as conic sections formed when a plane intersects a cone. The parabola is formed when the plane intersects the face of the cone and has an angle with respect to the axis of symmetry of the cone.
The point of intersection of the axis of symmetry and the parabola is the vertex. The vertex is the extreme point of the parabola. If the parabola opens upwards, the vertex is the lowest point and if the parabola opens downwards, the vertex is the highest point.
Important characteristics of a parabola
The main characteristics of a parabola are:
- The focus of the parabola is always located on the inside of the curve.
- The directrix is always located on the outside of the curve.
- The distance from any point on the parabola to the focus is the same as the distance from that point to the directrix.
- The vertex is the extreme point of the parabola. It can be the lowest or highest point of the parabola.
- The axis of symmetry crosses through the vertex.
Equation of the parabola
The equation for the parabola can vary depending on whether the parabola is centered at the origin or centered outside the origin. In addition, we can also obtain different variations of the parabola depending on whether it is oriented horizontally or vertically.
• If the parabola is centered at the origin and oriented vertically, its equation is $latex {{x}^2}=4ay$, where, a is the distance from the vertex to the focus.
• When the parabola is centered at the origin and oriented horizontally, its equation is $latex {{y}^2}= 4ax$.
• If the parabola is centered outside the origin and oriented vertically, its equation is $latex {{(x-h)}^2} = 4a (y-k)$, where $latex (h, ~k)$ are the coordinates of the vertex of the parabola.
• When the parabola is centered outside the origin and oriented horizontally, its equation is $latex {{(y-k)}^2}=4a(x-h)$.
See also
Interested in learning more about parabolas? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
