Free fall is the vertical motion of an object under the exclusive influence of gravitational force. In the absence of other forces such as air resistance, all objects fall with the same acceleration, known as the acceleration of gravity (g), whose approximate value near the earth’s surface is 9.8 m/s².
The equations describing the free fall motion are:
- Position equation: y = y₀ + v₀t + (1/2)at²
- Velocity equation: v = v₀ + at
- Acceleration equation: a = g = 9.8 m/s² (near earth surface)
Solved Exercises on Free Fall
EXERCISE 1
In the famous leaning tower of Pisa, in Italy, Galileo Galilei made his famous free fall experiments between 1589 and 1592. In them, he determined that all objects, regardless of their mass, take the same time to fall when dropped from the same height. He verified that an iron ball and a wooden ball, dropped simultaneously, reach the ground at the same time.

From there it is known that all bodies subject primarily to the earth’s gravitational attraction move with the same acceleration, the well-known acceleration of gravity, which is denoted by the letter $latex g$. In cases where the air resistance is significant or comparable to the force of terrestrial gravitation, then the acceleration of fall is less than $latex g$.
If an iron or wooden ball is dropped from the top of the Tower of Pisa, which is 55.86 m high, it takes 3.3764 seconds to reach the ground. Determine the value of the acceleration of gravity in $latex \frac{m}{s^2}$ and in $latex \frac{ft}{s^2}$.
Solution
Free fall is a rectilinear motion with constant acceleration, where the acceleration comes from the gravitational attraction of the Earth. The vertical coordinate $latex y$ changes with time $latex t$ as the body descends, which is why the vertical position is said to be a function of time given by the following expression:
$$ y(t)= h + v_0 \cdot t + \frac{1}{2} \cdot (-g) \cdot t^2 $$

In the previous expression, $latex h$ represents the initial height, $latex v_0$ the initial speed which, in the case of an object that is released, is zero ($latex v_0=0$). $latex g$ is the magnitude of the acceleration of gravity, a minus sign has been placed because that acceleration always points downward, and since the Y axis has a positive upward orientation, then downward is negative. The position of the ball at any time $latex t$ is given by $latex y(t)$ and is measured from the ground up to the current position of the ball.
Suppose that the ball reaches the ground at instant $latex t_s$, then for that instant it is true that $latex y(t_s)=0$:
$$ 0= h – \frac{1}{2} \cdot g \cdot {t_s}^2 $$
We solve for the acceleration of gravity $latex g$:
$$g=\dfrac{2 \cdot h}{{t_s}^2}$$
Using the known data to determine the numerical value of $latex g$:
$$g=\dfrac{2 \cdot 55.86 m}{{3.3764s}^2}=9.80 \frac{m}{s^2}$$
Taking into account that $latex 1m = 3.28084~ feet$, the acceleration of gravity expressed in feet per seconds squared is:
$$ g= 9.80 \frac{m}{s^2} = 9.80 \frac{3.28084~ feet}{s^2}=32.15 \frac{feet}{s^2}$$
EXERCISE 2
From the top of the tower of Pisa, a ball is thrown upwards giving it an initial impulse that gives it a speed of $latex v_0=10 \frac{m}{s}$. Calculate how long it takes the ball to reach the ground and what speed it has just at the instant it is arriving.
Solution
We choose a coordinate system with the origin at ground level and positive Y-axis direction upwards, in this case the position of the ball as a function of time is given by:
$$ y(t)= h + v_0 \cdot t + \frac{1}{2} \cdot (-g) \cdot t^2 $$
At the instant $latex t_s$, the ball reaches the ground. Using the known data, we are left with:
$$ 0= 55.86 + 10 \cdot t_s – \frac{1}{2} \cdot 9.80 \cdot {t_s}^2 $$
Note that the time $latex t_s$ satisfies a second-degree equation whose solutions are:
$$t_s= \dfrac{-10 \pm \sqrt{10^2 – 4 \cdot (-9.80/2) \cdot 55.86}}{2 \cdot (-9.80/2)}$$
$$ t_s= \dfrac{-10 \pm \sqrt{100 +1094.86}}{ -9.80} $$
This equation has two solutions, but we are only interested in the positive solution (the one with the negative sign in front of the root), which is after the operations have been performed:
$$ t_s=4.55 s$$
The velocity of the ball, just before touching the ground, is given by:
$$ v(t_s)=v_0-g \cdot t_s= 10 -9.80 \cdot 4.55= -34.59 \frac{m}{s}$$
Where the negative sign in the velocity result indicates that the velocity of the ball just before hitting the ground is pointing downwards.
EXERCISE 3
A bridge is 40 m above the surface of the river and a stone is dropped from the bridge. One second later, a second stone is thrown down and both reach the surface of the water simultaneously. Calculate the velocity with which the second stone was thrown and plot the situation ( Approximate the acceleration of gravity to the value 10 m/s2 ).
Solution
The Y axis is chosen with origin on the surface of the river and vertical direction upwards. The expressions that give the coordinate Y of each of the stones are:
$$ y_1(t) = h -\frac{1}{2} \cdot g \cdot t^2$$
$$y_2(t)= h \; – \; v_0 \cdot (t-t_o) -\frac{1}{2} \cdot g \cdot (t-t_o)^2$$
We know that when the stones reach the water surface of the river, their coordinate Y is zero. Using the known data we have:
$$ 0 = 40 -\frac{1}{2} \cdot 10 \cdot t_s^2$$
$$0= 40 \; – \; v_0 \cdot (t_s-1) -\frac{1}{2} \cdot 10 \cdot (t_s-1)^2$$
From the first equation, we obtain the arrival time $latex t_s$:
$$ t_s= \sqrt{8} s=2.83 s$$
Then we substitute this result in the second expression and solve for the velocity $latex v_0$:
$$0= 40 \; – \; v_0 \cdot (1.83) -\frac{1}{2} \cdot 10 \cdot (1.83)^2 \; \Rightarrow \; 23.26 \; – \; v_0 \cdot 1.83=0 $$
From where we obtain the value of the velocity with which the second stone was thrown:
$$ v_0=12.71 \frac{m}{s} $$
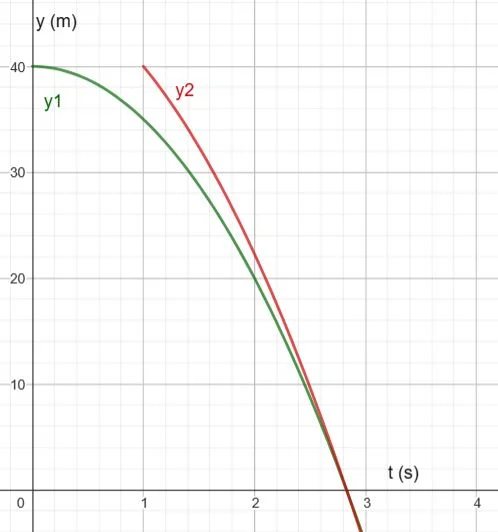
EXERCISE 4
A rocket starts from the ground and rises with a net upward acceleration of $latex 0.2\frac{m}{s^2}$ during the time of 40 seconds in which the propellant is consumed. Then, it continues to rise by inertia to a certain height and begins to descend until it reaches the ground again. Determine the maximum height reached by the rocket and the total time of its flight.
Solution
First, we will determine the height and velocity of the rocket 40 seconds after it was fired. For this, we will use a coordinate system with the Y-axis pointing upwards and originating at the ground.
Then, if the time t is between 0s and 40s the position of the rocket is given by:
$$ y(t)= \frac{1}{2} \cdot a \cdot t^2$$
It follows that the altitude reached at 40s of flight was:
$$ y(40s)= \frac{1}{2} \cdot 0.2 \cdot 40^2=160m$$
Reaching a speed of:
$$ v(40s) = 0.2 \frac{m}{s^2} \cdot 40 s= 8 \frac{m}{s}$$
After 40 seconds, all subsequent motion occurs at the acceleration of gravity, which we will approximate to $latex 10 \frac{m}{s^2}$.
The maximum height will occur when the speed is canceled for an instant, and we will call that instant $latex \tilde{t}$:
$$ v(\tilde{t})= 8 \frac{m}{s} – 10 \frac{m}{s^2} \cdot (\tilde{t}-40s)^2 = 0 \; \Rightarrow \tilde{t}=40.89s$$
The maximum height reached will be:
$$h_{max}=160m + 8 \frac{m}{s} \cdot 0.89s- \frac{1}{2} \cdot 10 \frac{m}{s^2} \cdot (0.89s)^2$$
$$ h_{max}=160.16 m$$
The time it takes to descend from the maximum altitude is: $latex t_{des}=\sqrt{\dfrac{2 \cdot 160.16}{10}}=5.66s$
Then the total flight time was: $latex t_v=40.89s + 5.66s=46.55s$
EXERCISE 5
A flowerpot falls from a window located 20 meters above the ground. Determine the speed with which it hits the ground and the time it takes.
Solution
Using the free fall formulas, we can calculate the final velocity ($latex v_f$) and time ($latex t$) as follows:
- $latex v_f = \sqrt{2 * g * h}$
- $latex t =\sqrt{2 * h / g}$
- Substituting the values, we obtain:
- $latex v_f = \sqrt{2 * 9.8 * 20} ≈ 19.8 m/s$
- $latex t = \sqrt{2 * 20 / 9.8} ≈ 2.02 s$
.
EXERCISE 6
A stone is dropped from the terrace of a building and is observed to take 6 seconds to reach the ground. Calculate the height of the terrace.
Solution
Using the free fall formula, we can calculate the height (h) of the terrace as follows:
- $latex h = 0.5 * g * t^2$
- Substituting the values, we obtain:
- $latex h = 0.5 * 9.8 * 6^2 ≈ 176.4 ~meters$
.
EXERCISE 7
A ball is thrown vertically upwards with an initial velocity of 15 m/s. Calculate the time it takes to reach its maximum height.
Solution
Using the free fall formula, we can calculate the time (t) it takes for the ball to reach its maximum height as follows:
- $latex v_f = v_i – g \cdot t$
- When the ball reaches its maximum height, its final velocity $latex v_f$ is equal to 0. Substituting the values, we obtain:
- $latex 0 = 15 \; – 9.8 \cdot t$
- $latex t = 15 / 9.8 ≈ 1.53 s$
.
EXERCISE 8
A ball is thrown vertically upwards with an initial velocity of 20 m/s. Calculate the maximum height it reaches.
Solution
Using the free fall formula, which relates final velocity, initial velocity and height, we can calculate the maximum height (h) reached by the ball as follows:
- $latex {v_f}^2 = {v_i}^2 – 2 \cdot g \cdot h$
- When the ball reaches its maximum height, its final velocity ($latex v_f$) is equal to 0. Substituting the values, we obtain:
- $latex 0 = 20^2 – 2 * 9.8 * h$
- $latex h = 20^2 / (2 * 9.8) ≈ 20.41 ~meters$
.
EXERCISE 9
A ball with an initial velocity of 25 m/s is thrown vertically upward from a height of 10 meters. Calculate the time it takes to reach the ground. (Approximate the acceleration of gravity to $latex 10 ~m/s^2$).
Solution
We will use the expression that gives the vertical position as a function of time for a motion with constant acceleration equal to the acceleration of gravity. We will choose the Y-axis pointing upwards and originating at the ground:
$$y(t)=y_0+v_0 \cdot t – \frac{1}{2} g \cdot t^2 $$
If we denote by $latex \tilde t$ the instant at which the ball reaches the ground ($latex y(\tilde t)=0$), we are left with:
$$0=10+25 \cdot \tilde t – \frac{1}{2} 10 \cdot {\tilde t}^2 $$
This is a quadratic equation that has two solutions: i) $latex \tilde t=-0.372s$ and ii) $latex \tilde t=+5.372s$. The first corresponds to a time before the ball was thrown, therefore it has no physical meaning. On the other hand, the second solution corresponds to the instant the ball hits the ground: $latex \tilde t=5.372s$
EXERCISE 10
A stone is dropped from the top of a cliff and the sound of the impact is heard 3 seconds later. If the speed of sound in air is 340 m/s, determine the height of the cliff.
Solution
We choose a coordinate system with the Y axis vertically upwards and the origin at the bottom (base) of the cliff. Thus, the position of the stone as a function of time, measured from the instant it was released, is given by:
$$y(t)=y_0-\frac{1}{2}g \cdot t^2$$
If we call $latex t^*$ the instant that the stone reaches the ground, and taking into account that for that instant the position (height) of the stone is zero we have:
$$y(t^*)=0=y_0-\frac{1}{2}g \cdot {t^*}^2$$
The above equation has two unknowns, which are the time $latex t^*$ and the height of the cliff $latex y_0$.
On the other hand, the time $latex t_s$ it takes for the sound to go from the bottom to the top of the cliff is:
$$ t_s= \dfrac{y_0}{V_s}$$
We also know that the time elapsed from the time the stone was released until the sound of the impact was heard is:
$$T=t^*+t_s=3s \; \Rightarrow \; {t^*}^2=(T-t_s)^2$$
Combining these equations we are left with:
$$\dfrac{2y_0}{g}=(T-\dfrac{y_0}{V_s})^2$$
Expanding the square and simplifying, we are left with the following quadratic equation in the variable $latex y_0$, which is just the height of the cliff:
$$\frac{1}{{V_s}^2}{y_0}^2-(\frac{2}{g}+\frac{2T}{V_s})y_0+T^2=0$$
Substituting the known data we are left with:
$$8.65 \cdot 10^{-6}{y_0}^2 – 0.2217 y_0 +9 =0$$
Solving the quadratic equation we have that the height of the cliff is:
$$y_0=40.66m$$
Free fall – Practice problems


Write the answer in the input box.
See also
Interested in learning more about motion in physics? You can take a look at these pages:




