Projectile motion studies the trajectory of an object thrown into the air with an initial velocity and a given angle, considering the acceleration of gravity. This type of motion combines two components: uniform horizontal motion and uniformly accelerated vertical motion.
The most important formulas for describing projectile motion are:
- Range: $latex R = \frac{v_{0}^2 \times \sin(2\theta)}{ g}$
- Maximum height: $latex h = \frac{v_{0}^2 \times \sin^2(\theta)}{ 2g}$
- Time: $latex t = \frac{2v_{0} \times \sin \theta}{g}$
- Horizontal position: $latex x = v_{0} \times \cos \theta \times t$
- Vertical position: $latex y = v_{0} \times \sin\theta \times t – (\frac{1}{2})gt^2$
Where, v₀ is the initial velocity, θ is the launch angle, g is the acceleration of gravity (9.8 m/s²) and t is the time.
Solved exercises on projectile motion
EXERCISE 1
A rescue plane flies horizontally over an isolated area at 100 m altitude, carrying a speed of 40 m/s. If it drops a package of supplies:
a) How long does it take for the package to reach the ground?
b) With what speed does it land?
c) How far horizontally does it fall, measured from the point where it was released?
Important
For this and the following exercises, air resistance is not considered and $latex g= 9.8\hspace{1mm}\dfrac{m}{s^2}$ is used, unless otherwise stated.
Solution
a) For a given altitude, the flight time is:
$$h=\frac{1}{2}gt^2$$
$$t=\sqrt{\frac{2h}{g}}$$
Substituting the values $latex h= 100\hspace{1mm}m$ and $latex g=9.8\hspace{1mm}\dfrac{m}{s^2}$, it results:
$$t=\sqrt{\frac{2\times 100\hspace{1mm}m }{9.8\hspace{1mm}\dfrac{m}{s^2}}}=4.5\hspace{1mm}s$$
b) The equation for the velocity vector as a function of time is:
$$\vec{v}(t)=v_0\hat{ i} – gt \hat{j}$$
The negative direction is downward, and the velocity components are:
$latex v_{x}=v_0=40\hspace{1mm}\dfrac{m}{s}$
$latex v_y=gt=9.8\hspace{1mm}\dfrac{m}{s^2}\times 4.5\hspace{1mm}s=44.1\hspace{1mm}\dfrac{m}{s}$
Therefore:
$$\vec{v}(t)=40\hat{ i} – 44.1 \hat{j}\hspace{1mm}\frac{m}{s}$$
The magnitude of the final velocity is:
$$v=\sqrt{40^2+(-44.1)^2}\hspace{1mm}\frac{m}{s}=59.5\hspace{1mm}\frac{m}{s}$$
c) The horizontal range is calculated by:
$latex x_{max}=v_x\cdot t_{flight}$
Substituting values:
$$ x_{max}=40\hspace{1mm}\frac{m}{s}\times 4.5\hspace{1mm}s=180\hspace{1mm}m$$
EXERCISE 2
A boy throws his key ring horizontally from the window of his house, being received by his friend, located in front of the window and at a horizontal distance of 4.8 m. The key ring flew through the air for 0.8 s and the friend’s hands on receiving it were 1.2 m above the floor.
With this information, find the following:
a) How high off the ground did the key ring depart?
b) The speed with which it reached the friend’s hands.
Solution
a) Let $latex y_0$ be the height from which the key ring starts, which did not descend completely, since it lacked 1.2 m, since it was caught by the friend. The vertical position is set as:
$$y=y_0-\frac{1}{2}gt^2$$
Substituting values:
$$1.2=y_0-\frac{1}{2}gt^2\Rightarrow y_0=\left(1.2+\frac{1}{2}\times 9.8\times 0.8^2\hspace{1mm}\right)m=4.34\hspace{1mm}m$$
b) First, the velocity components are calculated:
Horizontal component
$$v_x=\frac{x}{t}=\frac{4.8\hspace{1mm}m}{0.8\hspace{1mm}s}=6.0\hspace{1mm}\frac{m}{s}$$
Vertical component
$$v_y=gt=9.8\hspace{1mm}\frac{m}{s}\times 0.8\hspace{1mm}s =7.8\hspace{1mm}\frac{m}{s}$$
The velocity vector is:
$$\vec{v}(t)=6.0\hat{ i} – 7.8 \hat{j}\hspace{1mm}\frac{m}{s}$$
EXERCISE 3
A child rolls his toy car onto a table 74.0 cm high, projecting it horizontally so that it flies off the edge. The toy lands at a horizontal distance of 97.0 cm from the edge of the table. Calculate:
a) What was the speed with which the toy was projected over the table?
b) With what speed did it hit the ground?
b) At what angle did the toy hit the ground?
Solution
a) From the equation for the horizontal range, the velocity $latex v_0$ with which the toy was initially projected can be calculated:
$$x_{max}=v_{0x}t=v_0t$$
However, we first need to know the time it took to fall. This can be determined from the height of the table:
$$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times 74.0\hspace{1mm}cm}{981\hspace{1mm}\dfrac {cm}{s^2}}}=0.39\hspace{1mm}s$$
Knowing the time and the horizontal range of the projectile, which is 97.0 cm according to the statement, the horizontal velocity with which the toy was projected is:
$$x_{max}=v_{0x}t=v_0t\Rightarrow v_{0}=\frac{x_{max}}{t}=\frac{97.0\hspace{1mm}cm}{0.39\hspace{1mm}s}=248.7\hspace{1mm}\frac{cm}{s}$$
It remains constant throughout the motion.
b) The vector equation for the velocity at any instant of motion is:
$$\vec{v}(t)=v_0\hat{ i} – gt \hat{j}$$
It is assigned the negative downward direction.
The horizontal component of the velocity remains constant throughout the motion, and we only need to know the vertical component of the velocity upon reaching the ground.
Calculation of the vertical component of the velocity.
$$v_y=gt\Rightarrow v_y=981\hspace{1mm} \frac{cm}{s^2}\times 0.39\hspace{1mm}s=382.6\hspace{1mm} \frac{cm}{s}$$
Calculation of the final velocity vector.
The results obtained are substituted into the equation for the velocity:
$$\vec{v}(t)=248.7\hat{ i} – 382.6 \hat{j}\hspace{1mm} \frac{cm}{s}$$
The magnitude of the velocity on reaching the ground is:
$$v=\sqrt{248.7^2+(-382.6)^2}\hspace{1mm}\frac{cm}{s}=456\hspace{1mm}\frac{cm}{s}$$
c) The angle formed by the velocity vector with the positive horizontal axis is:
$$\theta =\arctan \frac{v_y}{v_x}=\frac{-382.6}{248.7}=-57º$$
This means that the velocity forms an angle of approximately 57º below the horizontal when the toy impacts the floor.
EXERCISE 4
A projectile with an initial velocity of 50 m/s is launched obliquely, forming a 30º angle with the horizontal, which falls later, at the same level of the starting point. Calculate the following:
a) Time it takes to reach maximum height.
b) Maximum height
c) Flight time.
d) Horizontal range.
e) Speed at which it reached the ground.
Solution
a) When the object reaches its maximum height, the vertical velocity $latex v_y$ cancels out, and then reverses its direction. In this case:
$$v_y=v_{0y}-gt_{max}=0$$
Where $latex t_{max}$ is the time it takes for the projectile to reach that maximum height. Therefore:
$$t_{max}=\frac{v_{0y}}{g}=\frac{50\hspace{1mm}\dfrac{m}{s}\times sin 30º}{9.8\hspace{1mm}\dfrac{m}{s^2}}=2.6\hspace{1mm}s$$
b) The maximum height is calculated by:
$$y_{max}=\frac{1}{2}gt_{max}^2=\frac{1}{2}\times 9.8\hspace{1mm}\dfrac{m}{s^2}\times (2.6\hspace{1mm}s)^2=33.1\hspace{1mm}m$$
c) Since the projectile falls further forward and at the same level as the ground, the maximum time is:
$$t_{flight}=2\cdot t_{max}=2\times2.6\hspace{1mm}s=5.2\hspace{1mm}s$$
d) The maximum horizontal range, $latex x_{max}$, is given by:
$$x_{max}=v_{0x}\cdot t_{flight}=v_{0}\cos 30º\cdot t_{flight}$$
$$x_{max}=50\hspace{1mm}\frac{m}{s}\times cos 30º\times 5.2\hspace{1mm}s=225.2\hspace{1mm}m$$
EXERCISE 5
The pirates fire a projectile from a 150 m. cliff with an inclination of 25º with respect to the horizontal and an initial speed of 200 m/s.
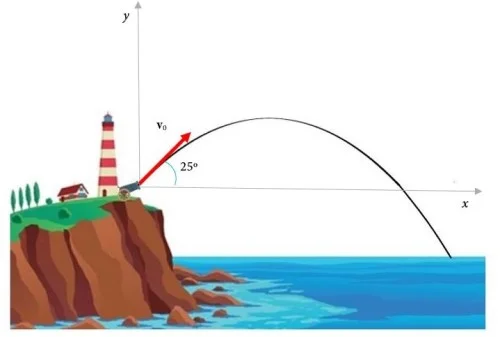
Calculate:
a) Flight time.
b) The maximum height attained by the projectile, measured from the sea surface.
c) The horizontal distance measured from the launching point to where the projectile falls into the sea.
Solution
a) In vector form, the position as a function of time $latex \vec {r}(t)$ is given by:
$$\vec {r}(t)=(x_0+v_{0x}t)\hat i +\left[y_0+v_{0y}t-\frac{1}{2}gt^2\right]\hat j$$
In the vertical, the negative direction is chosen downward. Choosing $latex x_0=0$ and $latex y_0=0$, the position remains:
$$\vec {r}(t)=v_{0x}t\hspace{1mm}\hat i +\left[v_{0y}t-\frac{1}{2}gt^2\right]\hat j$$
Then, for the following calculations, it is necessary to determine the components of the initial velocity:
$latex v_{0x}=v_0\cos 25º = 200\times \cos 25º\hspace{1mm}\dfrac{m}{s}=181.3\hspace{1mm}\dfrac{m}{s}$
$latex v_{0y}=v_0\cos 25º = 200\times \sin25º\hspace{1mm}\dfrac{m}{s}=84.5\hspace{1mm}\dfrac{m}{s}$
The flight time is obtained from the vertical component of the position equation, since when falling into the sea, the projectile must be in the position $latex y = -150\hspace{1mm}m$, then:
$$v_{0y}t-\frac{1}{2}gt^2=-150$$
Substituting the known values, we obtain a second-degree equation for time:
$$84.5t-4.9t^2=-150$$
$$4.9t^2-84.5t-150=0$$
Whose solutions are:
$latex t_1=-1.6$
$latex t_2=18.9$
Only the second solution makes sense. Therefore, the projectile travels $latex 18.9\hspace{1mm}s$ from the cliff to the sea.
b) The maximum height with respect to the starting point on the cliff, can be calculated through:
$$y_{max}=\frac{v_{0y}^2}{2g}$$
Substituting values:
$$y_{max}=\frac{\left(84.5\hspace{1mm}\dfrac{m}{s}\right)^2}{2\times 9.8\hspace{1mm}\dfrac{m}{s^2}}=364.3\hspace{1mm}m $$
To find the maximum height above sea level, the 150 m height of the cliff is added:
$$H_{max}=364.3\hspace{1mm}m+150.0\hspace{1mm}m=514.3\hspace{1mm}m$$
c) The horizontal range is determined from:
$$x_{max}=v_{0x}\cdot t_{flight}=$$
$$x_{max}=181.3\hspace{1mm}\frac{m}{s}\times18.9\hspace{1mm}s=3426.6\hspace{1mm}m$$
EXERCISE 6
A piece of ice is sliding on a roof inclined at 37º below the horizontal. When it reaches the edge, it has a speed of 8.6 m/s and is 10 m above the level of the sidewalk.
a) Will it fall on top of a 6-foot tall man, who is standing at a horizontal distance of 1.20 m from the edge of the roof?
b) If it does not reach it, where will the piece of ice fall?
Solution
a) The components of the initial velocity of the ice chunk are:
$latex v_{0x}=8.6\times\cos 37º \hspace{1mm}\dfrac{m}{s}=6.9\hspace{1mm}\dfrac{m}{s}$
$latex v_{0y}=-8.6\times\sin 37º \hspace{1mm}\dfrac{m}{s}=-5.2\hspace{1mm}\dfrac{m}{s}$
The vertical component is negative since the roof is inclined downward.
The origin of coordinates is taken right at the edge of the roof, where the piece of ice starts its parabolic motion. The vertical downward direction is negative.
If the person measures 1.80 m, measured from the ground up, it means that the top of his head is in the $latex position ~y=(1.8-10)\hspace{1mm}m = -8.2\hspace{1mm}m$ , with respect to the origin of coordinates.
In addition, the statement says that the man is at a horizontal distance from the edge of the roof equal to 1.2 m. Therefore, the coordinates of the top of his head are:
$$(1.2;-8.2)\hspace{1mm}m$$
If this point belongs to the parabolic trajectory of the ice chunk, it hits the man, but if it does not belong, it does not hit him.
The position of the ice chunk at any instant $latex t$ is given by:
$latex x(t)=6.9t$
$latex y(t)=-5.2t-4.9t^2$
Let’s find out at what instant of time the piece of ice is located at the position $latexx=1.2\hspace{1mm} m$:
$$t=\frac{1.2\hspace{1mm}m}{6.9\hspace{1mm}\dfrac{m}{s}}= 0.174\hspace{1mm}s$$
If the vertical position at this instant is equal to -8.2 m, it falls on the man’s head, otherwise it does not hit him:
$latex y(0.174)=[-5.2\times 0.174 -4.9(0.174)^2]\hspace{1mm}=-1.05\hspace{1mm} m$
It is concluded that it does not hit him. In fact, the piece of ice is quite a distance above the man’s head and still needs to reach the ground, in the position $latex y = -10\hspace{1mm}m$.
b) To know at what point on the ground the piece of ice lands, it is necessary to know the time of flight, putting $latex y =-10\hspace{1mm}m$ in the equation for the vertical position:
$latex -10=-5.2t-4.9t^2$
A second-degree equation for time is obtained:
$$ 4.9t^2+5.2t+10=0$$
The positive solution is:
$$t=0.99332\hspace{1mm}s$$
For this time, the horizontal coordinate of the ice chunk is:
$$ x(t)=6.9\times 0.99332\hspace{1mm}m=6.9\hspace{1mm}m$$
The person had no reason to worry about the ice falling on him, as it actually landed much farther ahead.
EXERCISE 7
A projectile is launched with an initial speed of $latex \vec {v}_0=10\hat i +5\hat j\hspace{1mm}\dfrac{m}{s}$ and, after a time, its speed is $latex \vec {v}(t)=10\hat i +0\hat j\hspace{1mm}\dfrac{m}{s}$. Determine:
a) For that instant, the position of the projectile with respect to the launching point.
b) Launch angle.
c) The speed after t = 1.5 s. Is the object up or down?
d) If the object was projected from a height of 6 m above the ground, what will be its horizontal range?
Solution
a) The origin of the coordinate system is located at the launch point. At the unknown instant for which the velocity is given, the projectile must have reached its maximum height with respect to the origin, since the vertical component of the velocity is zero.
Given that:
$$v_y^2=v_{0y}^2-2gy_{max}\Rightarrow y_{max}=\frac{v_{0y}^2}{2g}$$
From the initial velocity vector, which we know is $latex \vec {v}_0=10\hat i +5\hat j\hspace{1mm}\dfrac{m}{s}$, it follows that:
$latex v_{0x}=10 \hspace{1mm}\dfrac{m}{s}$
$latex v_{0y}=5 \hspace{1mm}\dfrac{m}{s}$
Therefore, the vertical position at that time is:
$$y=y_{max}=\frac{(5 \hspace{1mm}\dfrac{m}{s})^2}{2\times 9.8 \hspace{1mm}\dfrac{m}{s^2}}=1.3\hspace{1mm}m$$
For the horizontal position:
$$x=v_{0x}\cdot t$$
The time is the maximum time, which is given by:
$$t_{max}=\frac{v_{0y}}{g}=\frac{5 \hspace{1mm}\dfrac{m}{s}}{9.8 \hspace{1mm}\dfrac{m}{s^2}}=0.51 \hspace{1mm}s$$
Which leads to:
$$x=10 \hspace{1mm}\dfrac{m}{s}\times 0.51 \hspace{1mm}s=5.1 \hspace{1mm}m$$
Putting together the previous results in the position vector $latex \vec r(t)$, we have:
$$\vec r(0.51)= \left(5.1 \hspace{1mm}\hat i +1.3\hspace{1mm}\hat j\right)\hspace{1mm}m$$
This is the position of the object with respect to the origin in t=0.51 s.
b) The launch angle $latex \theta$ is obtained from:
$$\theta =\arctan\left(\frac{v_{0y}}{v_{0x}}\right)=\arctan\left(\frac{5}{10}\right)=26.6º$$
c) The velocity vector $latex \vec v$ is given by:
$$\vec v(t) = v_x\hat i +v_y\hat j=v_{0x}\hat i+(v_{0y}-gt)\hat j$$
After t = 1.5 s, the vertical component of the velocity is:
$$v_y(1.5)=5-(9.8\times 1.5)\hspace{1mm}\frac{m}{s}=-9.7\hspace{1mm}\frac{m}{s}$$
Therefore:
$$\vec v(1.5) = (10.0\hat i -9.7\hat j)\frac{m}{s}$$
The object is going down, since the t= 1.5 s is greater than the maximum time. Furthermore, it can be seen that the sign of the vertical component of the velocity is negative.
d) To calculate the horizontal range, we need the flight time, which is not equal to twice the maximum time, since the launch is not at level, since the statement warns that it was projected at a height of 6 m above the ground.
In this case, the flight time is calculated when the mobile is at the vertical coordinate $latex y = -6\hspace{1mm}m$, which is assigned a negative sign because it is below the launch point
$$y(t)=v_{0y}t-\frac{1}{2}gt^2$$
Substituting values:
$$-6=5t-4.9t^2\Rightarrow 4.9t^2-5t-6=0$$
The positive solution is:
$$t=1.7\hspace{1mm}s$$
The maximum range is given by:
$$x_{max}=v_{0x}\cdot t_{flight}=10\hspace{1mm}\frac{m}{s}\times1.7\hspace{1mm}s= 17\hspace{1mm}m$$
EXERCISE 8
From a mound of 2 m height above the ground, a girl throws a ball with initial velocity of horizontal component equal to 15 m/s. During its flight, the ball passes just over the edge of a wall located 10 m from the launching point, whose height from the ground is 18 m.
a) What is the vertical component of the velocity?
b) At what angle was the ball projected?
c) How long does it take to reach the ground?
d) How far from the wall does it do so?
e) What was its final speed?
Solution
a) The launch point is located at the origin of the coordinate system, so it is at the point $latex (0.0)$. The ball passes just over the edge of the wall.
The coordinates of this point, with respect to the launching point, are: $latex (10.18-2)=(10.16)\hspace{1mm}m$ (2 m must be subtracted from the height of the wall, since the launching point is 2 m above the ground.
We start from the position equations:
$latex x(t)=v_{0x}t$
$latex y(t)=v_{0y}t-\frac{1}{2}gt^2$
Given that the point $latex (10,16)\hspace{1mm}m$ and the horizontal component of the velocity equal to 15 m/s are known, we obtain:
$latex 10=15t$
$latex 16=v_{0y}t-4.9t^2$
From the first equation results:
$$t=\frac{10}{15}\hspace{1mm}s=0.67\hspace{1mm}s$$
This is the time it takes for the ball to reach the edge of the wall.
Substituting it in the second equation, the vertical component of the velocity is obtained:
$latex v_{0y}=\dfrac{16+4.9t^2}{t}=\dfrac{16+4.9\times 0.67^2}{0.67}\hspace{1mm}\dfrac{m}{s}=27.2\hspace{1mm}\dfrac{m}{s}$
b) The launch angle of the ball is:
$$\arctan\left(\frac{v_{0y}}{v_{0x}}\right)=\arctan\left(\frac{27.2}{15}\right)=61.1º$$
c) The vertical coordinate of the landing point is $latex y=-2\hspace{1mm}m$, therefore, the flight time is calculated by solving the following quadratic equation:
$$-2=27.2t-4.9t^2$$
$$4.9t^2-27.2t-2=0$$
The positive solution is:
$$t_{flight}=5.6\hspace{1mm}s$$
d) The horizontal range is given by:
$latex x_{max}=v_{0x}\cdot t_{flight}$
Therefore:
$$x_{max}=15\hspace{1mm}\dfrac{m}{s}\times 5.6\hspace{1mm}s=84\hspace{1mm}m$$
Since the wall is 10 m from the launching point, measured horizontally, the ball falls at the next horizontal distance from it:
$$x_{wall}=(84 -10)\hspace{1mm}m=74\hspace{1mm}m$$
e) The horizontal component of the velocity remains unchanged during the whole movement, then:
$$v_x=v_{0x}=15\hspace{1mm}\frac{m}{s}$$
The vertical component is calculated knowing the flight time:
$$v_y=v_{0y}-9.8t=(27.2-9.8\times 5.6)\hspace{1mm}\frac{m}{s}=-27.7\hspace{1mm}\frac{m}{s}$$
therefore:
$$\vec v_{final}=\left(15\hspace{1mm}\hat i-27.7\hspace{1mm}\hat j\right)\hspace{1mm}\frac{m}{s}$$
EXERCISE 9
An object is launched at level at a certain angle, so that its horizontal range is five times its maximum height. Determine:
a) Launch angle.
b) The initial velocity required for the horizontal range to be 200 m.
c) Flight time.
Solution
a) Since the launch is level, the parabolic trajectory is symmetrical and $latex t_{flight}=2t_{max}$.
The maximum time is calculated by:
$$t_{max}=\frac{v_{0y}}{g}$$
Substituting into the equation for the horizontal range:
$$x_{max}=v_{0x}\left(2\frac{v_{0y}}{g}\right)=2v_{0}\cos\theta\frac{v_{0y}}{g}=\frac{2v_{0}^2\cos\theta\sin\theta}{g}=\frac{v_{0}^2\sin2\theta}{g}$$
The maximum height is:
$$y_{max}=\frac{v_{0y}^2}{2g}=\frac{v_{0}^2(\sin\theta)^2}{2g}$$
According to the statement, the horizontal range is 5 times the maximum height, so that we obtain:
$$x_{max}=\frac{2v_{0}^2\cos\theta\sin\theta}{g}=\frac{5v_{0}^2(\sin\theta)^2}{2g}$$.
Simplifying:
$$2\cos\theta=\frac{5}{2}\sin\theta\Rightarrow 5\sin\theta=4\cos\theta\Rightarrow \tan\theta=\frac{4}{5}$$
$$\theta=38.7º$$
b) Starting from:
$$x_{max}=\frac{2v_{0}^2\cos\theta\sin\theta}{g}$$
We solve for $latex v_0$ and substitute the numerical values:
$$v_{0}=\sqrt{\frac{gx_{max}}{2\cos\theta\sin\theta}}=\left(\sqrt{\frac{9.8\times 200}{2\cos 38.7º\sin 38.7º}}\right)\hspace{1mm}\frac{m}{s}=45.7\hspace{1mm}\frac{m}{s}$$
c) The flight time is calculated by substituting values in:
$$t_{flight}=2t_{max}=2\frac{v_{0y}}{g}=2\frac{v_{0y}}{g}=\frac{2\times45.7\times\sin 38.7º}{9.8}\hspace{1mm}s=5.8\hspace{1mm}s$$
EXERCISE 10
From the roof of a 55 m high building, a stone p with initial velocity 16 m/s is thrown horizontally, and at the same time, from the base of the building and just below the point where p is thrown, another stone q is thrown with initial velocity 32 m/s which forms an angle of 60º with the horizontal. Determine:
a) If the stones collide, at what instant do they do so?
b) The coordinates of the point where the stones collide.
c) Verify the previous results in graphical form.

Solution
a) To find out if the stones collide, first the position equations for each stone are posed.
The origin of coordinates must be placed at a convenient point. In this case, the q stone throwing point was chosen.
(Note: it can also be placed at the launching point of p, adjusting, the result will be the same).
Stone p: horizontal throw
$latex x_p=16t_p$
$latex y_p=55-4.9t_p^2$
Stone q: Throw at an angle
The components of its initial velocity are:
$latex v_{0x}=32\times\cos60º\hspace{1mm}\dfrac{m}{s}=16.0\hspace{1mm}\dfrac{m}{s}$
$latex v_{0y}=32\times\sin60º\hspace{1mm}\dfrac{m}{s}=27.7\hspace{1mm}\dfrac{m}{s}$
And their equations of position have the form:
$latex x_q=v_{0x}t_q=16t_q$
$latex y_q=v_{0y}t_q-4.9t_q^2=27.7t_q-4.9t_q^2$
If the stones meet, they will meet at the same time, so that $latex t_p=t_q=t$. Note that the horizontal components of the position of each stone are the same, since $latex x_p=x_q=16t$.
Then, the vertical components are equal:
$$y_p=y_q\Rightarrow 55-4.9t^2=27.7t-4.9t^2$$
Meaning:
$$27.7t=55\Rightarrow t=\frac{55}{27.7}\hspace{1mm}{s}=1.98 \hspace{1mm}{s} $$
The stones will collide after 1.98 sec.
b) The coordinates of the point where the stones collide are:
$$x=16\hspace{1mm}\frac{m}{s}\times 1.98 \hspace{1mm}{s}=31.75 \hspace{1mm}{m}$$
$$y=(55-4.9\times 1.98^2)\hspace{1mm}m=35.79\hspace{1mm}{m}$$
The stones are located at the point: (31.75; 35.79) m.
c) For this we, need to plot the trajectory $latex y(x)$ for each stone, in the same Cartesian system:
Trajectory of p
Stone p: horizontal throw
$latex x_p=16t\Rightarrow t=\dfrac{x}{16}$
$latex y_p=55-4.9t^2\Rightarrow y=55-4.9\left(\dfrac{x}{16}\right)^2=55-0.019x^2$
Stone q: Throw at an angle
$latex x_q=16t\Rightarrow t=\dfrac{x}{16}$
$latex y_q=\dfrac{27.7x}{16}-4.9\left(\dfrac{x}{16}\right)^2=1.73x-0.019x^2$
The graph below shows the intersection of the parabolic trajectories at the indicated point.

Projectile Motion – Practice Problems


Write the answer in the input box.
See also
Interested in learning more about motion in Physics? You can take a look at these pages:




