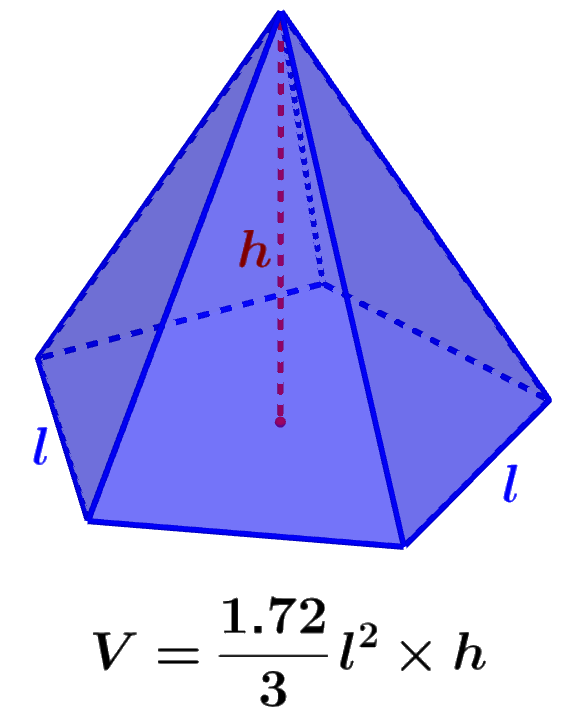
The volume of a pentagonal pyramid is calculated by multiplying the area of the pentagonal base by the length of the height of the pyramid. The surface area of the pentagonal pyramid is calculated by adding the areas of the pentagonal base and the lateral triangular faces.
Here, we will look at the formulas that we can use to calculate the volume and area of pentagonal pyramids. Then, we will apply these formulas to solve some practice problems.
How to find the volume of a pentagonal prism
The volume of any pyramid is calculated by multiplying the area of its base by its height and dividing the product by three. Therefore, we have the following formula:
$latex V=\frac{1}{3}\text{Area base}\times \text{Height}$
In turn, these pyramids have a pentagonal base and the area of a pentagon is calculated using the following formula:
$latex A=1.72{{l}^2}$
where l is the length of one of the sides of the pentagon.
This formula is derived by dividing the pentagon into five triangles and finding the area of each triangle separately.
Using the expression for the area of a given pentagon, the formula for the volume of a pyramid becomes:
| $latex V=\frac{1.72}{3}{{l}^2}h$ |
where l is the length of one of the sides of the pentagonal base and h is the length of the height of the pyramid.
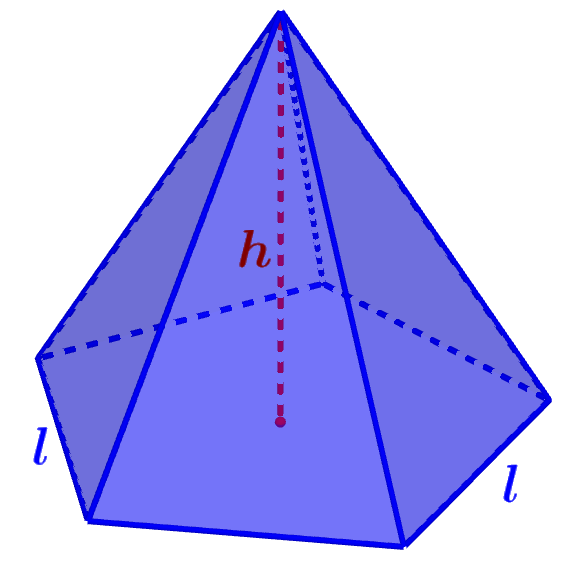
How to find the surface area of a pentagonal pyramid
The surface area is calculated by adding the areas of all the faces of a geometric figure. Pentagonal pyramids have one pentagonal face and five lateral triangular faces. To find the area of the pentagonal face, we use the following formula:
$latex A=1.72{{l}^2}$
where l represents the length of one of the sides of the pentagonal base.
On the other hand, the area of triangular faces is found by using the formula for the area of any triangle:
$latex A=\frac{1}{2}bh$
where b represents the length of the triangle’s base and h represents the height.
In pentagonal pyramids, the bases of the triangular faces are equal to the length of one of the sides of the base. Also, the five triangular faces are congruent. That means the formula for the surface area of these pyramids is:
$latex A_{s}=1.72{{l}^2}+5(\frac{1}{2}bh)$
$latex A_{s}=1.72{{l}^2}+(\frac{5}{2}lh)$
Volume and area of a pentagonal pyramid – Examples with answers
EXAMPLE 1
What is the volume of a pyramid that has a pentagonal base of 1 m and a height of 3 m?
Solution
We have the following:
- Sides of the pentagon, $latex l=1$
- Height, $latex h=3$
We use the volume formula with these values:
$latex V=\frac{1.72}{3}{{l}^2}h$
$latex V=\frac{1.72}{3}{{(1)}^2}(3)$
$latex V=\frac{1.72}{3}(1)(3)$
$latex V=1.72$
The volume is 1.72 m³.
EXAMPLE 2
What is the surface area of a pentagonal pyramid with a height of 5 m and sides of length 1 m?
Solution
From the question, we have the lengths $latex h=5$ and $latex l=1$. Using the volume formula with these values, we have:
$latex A_{s}=1.72{{l}^2}+\frac{5}{2}lh$
$latex A_{s}=1.72{{(1)}^2}+\frac{5}{2}(1)(5)$
$latex A_{s}=1.72+12.5$
$latex A_{s}=14.22$
The surface area is equal to 14.22 m².
EXAMPLE 3
A pentagonal pyramid has a base with sides of a length of 2 m and a height of 5 m. What is its volume?
Solution
We have these values:
- Sides of the pentagon, $latex l=2$
- Height, $latex h=5$
We substitute these values in the volume formula:
$latex V=\frac{1.72}{3}{{l}^2}h$
$latex V=\frac{1.72}{3}{{(2)}^2}(5)$
$latex V=\frac{1.72}{3}(4)(5)$
$latex V=11.47$
The volume is 11.47 m³.
EXAMPLE 4
If a pyramid has a height of 6 m and a pentagonal base with sides of 2 m, what is its surface area?
Solution
We look at the lengths $latex h=6$ and $latex l=2$. If we use these values in the volume formula, we have:
$latex A_{s}=1.72{{l}^2}+\frac{5}{2}lh$
$latex A_{s}=1.72{{(2)}^2}+\frac{5}{2}(2)(6)$
$latex A_{s}=6.88+30$
$latex A_{s}=36.88$
The surface area is equal to 36.88 m².
EXAMPLE 5
If a pentagonal pyramid has sides that are 3 m long and 6 m high, what is its volume?
Solution
We have the following:
- Sides of the pentagon, $latex l=3$
- Height, $latex h=6$
We use the volume formula with these values:
$latex V=\frac{1.72}{3}{{l}^2}h$
$latex V=\frac{1.72}{3}{{(3)}^2}(6)$
$latex V=\frac{1.72}{3}(9)(6)$
$latex V=30.96$
The volume is 30.96 m³.
EXAMPLE 6
What is the surface area of a pentagonal pyramid that has sides of 4 m and a height of 10 m?
Solution
We use the lengths $latex h=10$ and $latex l = 4$ in the volume formula. Therefore, we have:
$latex A_{s}=1.72{{l}^2}+\frac{5}{2}lh$
$latex A_{s}=1.72{{(4)}^2}+\frac{5}{2}(4)(10)$
$latex A_{s}=27.52+100$
$latex A_{s}=127.52$
The surface area is equal to 127.52 m².
EXAMPLE 7
A pyramid has a pentagonal base with sides of length 5 m and a height of 12 m. What is its volume?
Solution
From the question, we get the following lengths:
- Sides of the pentagon, $latex l=5$
- Height, $latex h=12$
If we substitute these values in the volume formula, we have:
$latex V=\frac{1.72}{3}{{l}^2}h$
$latex V=\frac{1.72}{3}{{(5)}^2}(12)$
$latex V=\frac{1.72}{3}(25)(12)$
$latex V=172$
The volume is 172 m³.
EXAMPLE 8
If a pentagonal pyramid has sides that are 6 m long and 12 m high, what is its surface area?
Solution
We substitute the lengths $latex h =12$ and $latex l=6$ in the formula for the surface area:
$latex A_{s}=1.72{{l}^2}+\frac{5}{2}lh$
$latex A_{s}=1.72{{(6)}^2}+\frac{5}{2}(6)(12)$
$latex A_{s}=61.92+180$
$latex A_{s}=141.92$
The surface area is equal to 141.92 m².
Volume and area of a pentagonal pyramid – Practice problems


What is the volume of a pentagonal pyramid with sides of length 6 m and height of length 13 m?
Write the answer using two decimal places.
See also
Interested in learning more about geometric pyramids? Take a look at these pages: