The Pythagorean theorem is the most used in trigonometry and allows us to calculate the length of one of the sides of a triangle if we know the length of the other two sides. On the other hand, the converse of the Pythagorean theorem allows us to determine whether a triangle is right, acute, or obtuse by comparing the sum of the squares of the two legs with the square of the hypotenuse.
In this article, we will look at a detailed definition of the converse of the Pythagorean theorem. Then, we will learn how to prove this theorem and apply it to solve some practice problems.
What is the converse of the Pythagorean theorem?
The converse of the Pythagorean theorem states, “If we have a²+b²=c² in a triangle with sides a, b, and c, the angle between a and b must be equal to 90° and the triangle is a right triangle.”
We can also use the converse of the Pythagorean theorem to determine whether a triangle is obtuse or acute. Therefore, for a triangle that has sides a, b, and c, where c is the hypotenuse, we have the following cases:
1. If we have c²<a²+b², the angle opposite side c is acute and the triangle is an acute triangle.
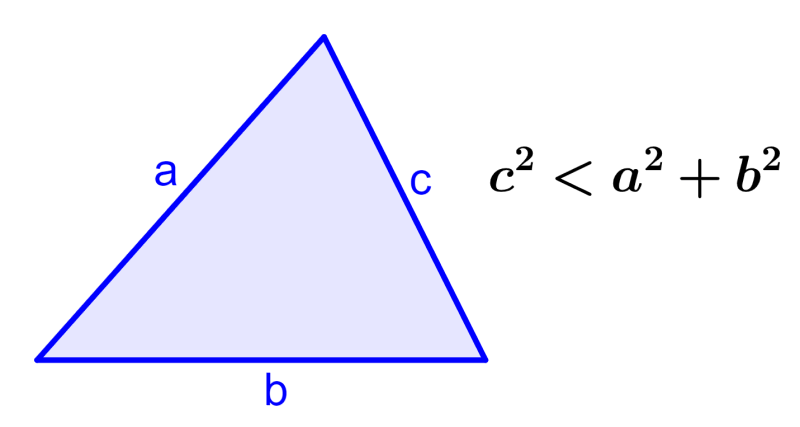
2. If we have c²=a²+b², the angle opposite side c is right and the triangle is a right triangle.
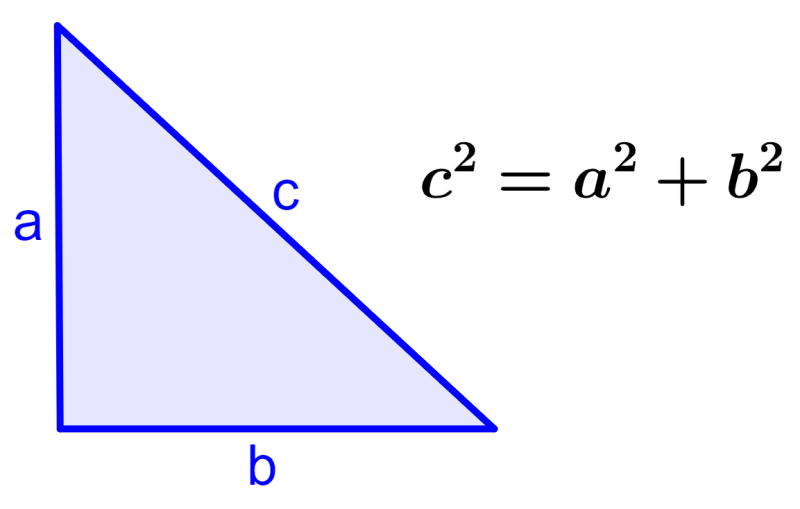
3. If we have c²>a²+b², the angle opposite side c is obtuse and the triangle is an obtuse triangle.
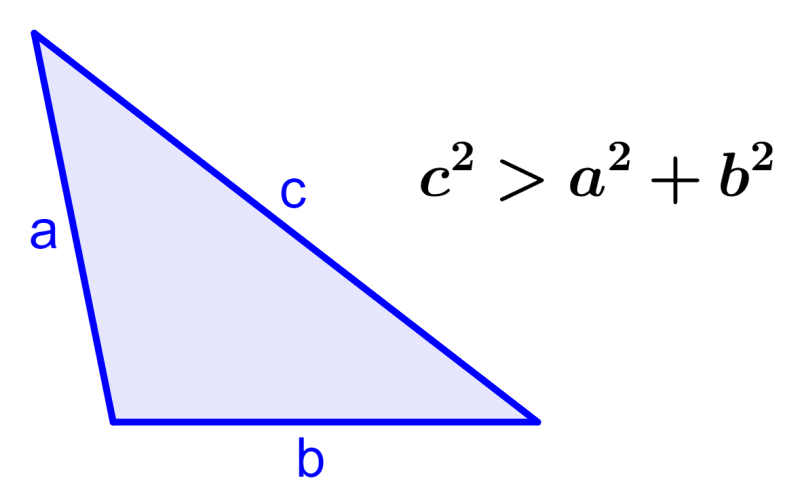
Proof of the converse of the Pythagorean theorem
To prove the converse of the Pythagorean theorem, we are going to use two triangles.
First, we have the triangle ABC, in which we have AC²=AB²+BC². To prove the converse theorem, we have to prove that ∠B=90°.
Then, we construct a right triangle DEF with a right angle at E. That is, we have ∠E=90°. Furthermore, this triangle fulfills the condition that DE=AB and EF=BC.
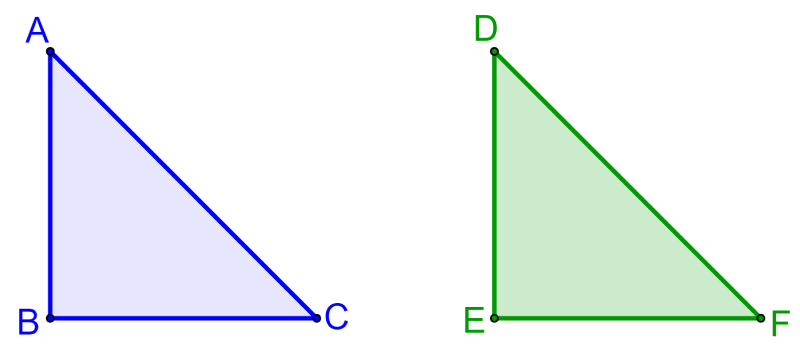
In triangle DEF, we can use the Pythagorean theorem since ∠E=90°. Therefore, we have:
DF² = DE² + EF²
Since DE=AB and EF=BC, we can substitute to get:
DF² = AB² + BC²
Since we have AC²=AB²+BC² from the first triangle, we can deduce that:
AC² = DF²
AC = DF
Therefore, we have that all the sides of the two triangles are equal. This means that the triangles ABC and DEF are congruent (by the SSS theorem).
Since the triangles are congruent, the corresponding angles are equal. Thus, we have:
∠B = ∠E
We know that angle E is equal to 90°, so angle B also measures 90° and we have proved the converse of Pythagoras’ theorem.
Converse of the Pythagorean theorem – Examples with answers
The following examples are solved using the converse of the Pythagorean theorem. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
A triangle has sides of lengths 3, 5, and 6 units. Determine whether the triangle is obtuse, right, or acute.
Solution
We can see that 6 is the longest side. Therefore, we can write:
c²=a²+b²
(6)²=(3)²+(5)²
36=9+25
36=34
Then, we have (6) ²> (3) ² + (5) ². This means that the triangle is obtuse.
EXAMPLE 2
A triangle has sides of lengths 6, 8, and 10 units. Is the triangle acute, obtuse, or right?
Solution
In this case, the longest side is 10. Therefore, we have:
c²=a²+b²
(10)²=(6)²+(8)²
100=36+64
100=100
Then, we have (10)²=(6)²+(8)². This means that the triangle is right.
EXAMPLE 3
Determine whether the triangle with sides 6, 7, 9 units long is acute, obtuse, or right.
Solution
The longest side is 9. Therefore, we have:
c²=a²+b²
(9)²=(6)²+(7)²
81=36+49
81=85
Then, we have (9)²<(6)²+(7)². This means that the triangle is acute.
EXAMPLE 4
Determine whether the triangle with sides 10, 12, 15 units long is right or not.
Solution
The longest side is 15. Therefore, we have:
c²=a²+b²
(15)²=(10)²+(12)²
225=100+144
225=244
This means that the triangle is not right.
Converse of the Pythagorean theorem – Practice problems
Apply what you have learned about the converse of the Pythagorean theorem and solve the following problems. Click “Check” to verify your answer.
See also
Interested in learning more about the Pythagorean theorem? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
