The interior angles of any triangle have a total sum of 180°. Based on the lengths of their sides, we can distinguish three types of triangles: equilateral, isosceles, and scalene. Depending on the type of triangle we have, we can use different methods to calculate the measures of the interior angles.
Here, we will learn how to calculate all the interior angles of equilateral, isosceles, and scalene triangles.
Sum of interior angles of a triangle
All triangles have a sum of interior angles equal to 180°. To verify this, we can use the following diagram:
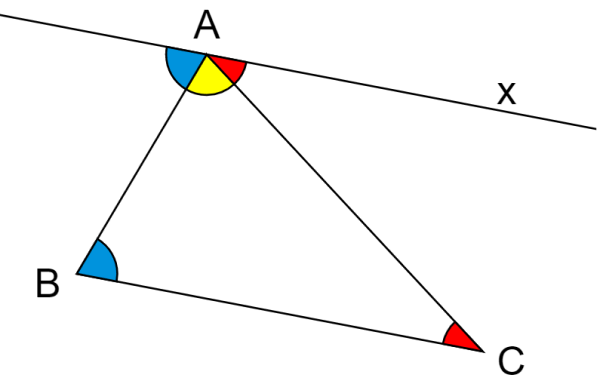
Each interior angle is represented in a different color. The line x drawn at the top vertex of the triangle is parallel to the base of the triangle. This means that we form corresponding angles. That is, the blue angles are the same and the red angles are also the same.
Therefore, in the top vertex, we have three angles that complete the straight line, so their sum must be equal to 180°.
Calculate the interior angles of an equilateral triangle
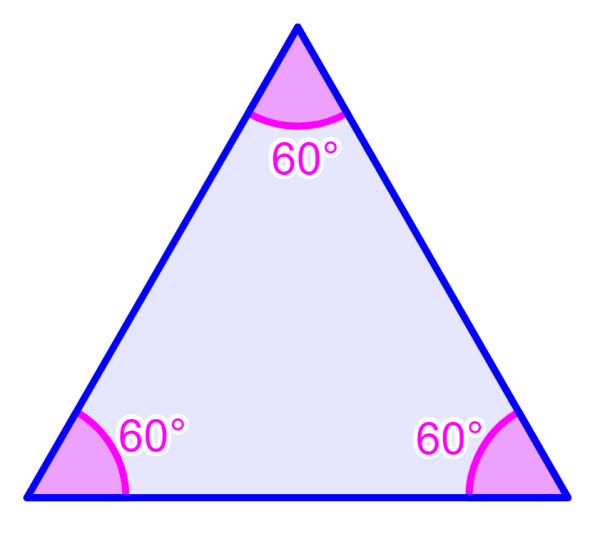
An equilateral triangle is characterized by having all the sides with the same length and all the internal angles with the same measure. We can find the measure of the interior angles of these triangles by remembering that all triangles have an angle sum of 180°.
Since the angles in an equilateral triangle are equal, we have to divide 180° by 3 to get the measure of an angle. Therefore, we have:
180°÷3 = 60°
Each of the interior angles of an equilateral triangle is equal to 60°.
Calculate the interior angles of an isosceles triangle
An isosceles triangle is characterized by having two sides with the same length and the third side with a different length. Furthermore, isosceles triangles also have two angles with the same measure and the third angle with a different measure.
Therefore, in order to determine the measure of all the interior angles of an isosceles triangle, we have to know the measure of at least one angle.
EXAMPLE 1
What are the measures of all the interior angles of the triangle below?
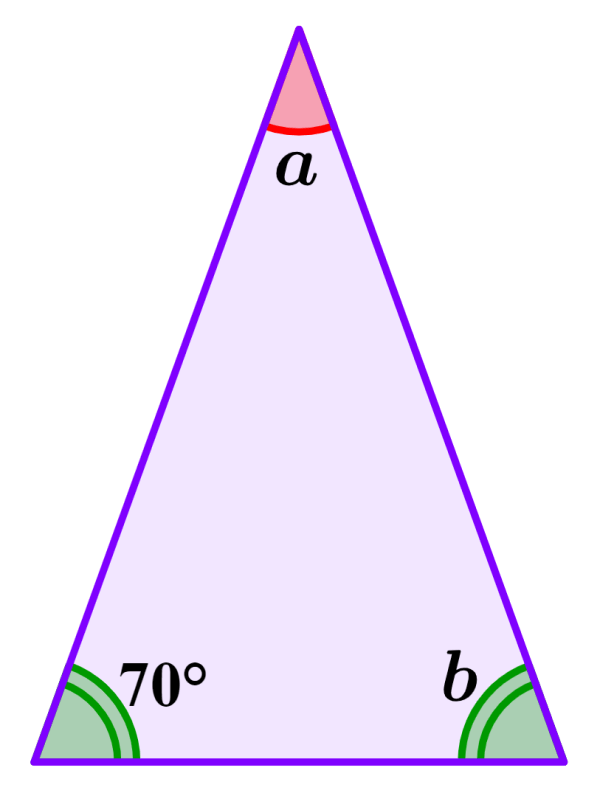
Solution: The angles that are represented by the double line are equal, so we have b=70°.
Now, to find the measure of the other angle, we add the known angles and subtract from 180°. Therefore, we have:
70°+70° = 140°
⇒ 180°-140° = 40°
The measure of angle a is 40°.
EXAMPLE 2
Determine the measures of the interior angles of the triangle below.
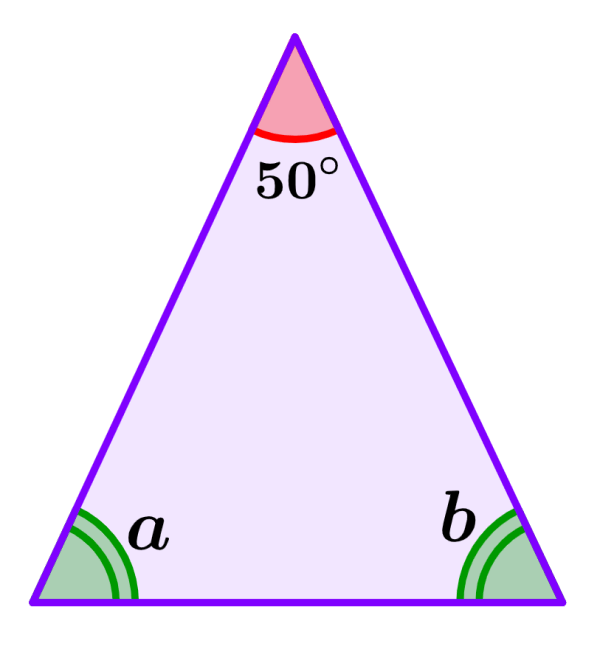
Solution: Angles a and b are equal since they are represented by the double line and have the same color. Therefore, we can find its measure by subtracting the known angle from 180° and then dividing by 2. Thus, we have:
180°-50° = 130°
Since both angles are equal, we divide the result by 2 to get the measure of an angle:
130°÷2 = 65°
The measure of angles a and b is 65°.
Calculate the interior angles of a scalene triangle
Scalene triangles are characterized by having all their sides with different lengths. This also means that all the interior angles of a scalene triangle have different measures. Therefore, in order to find the measure of an internal angle of a scalene triangle, we need to know the measures of the other two angles.
EXAMPLE 1
Find the missing angle of the triangle below.
Solution: In this case, we have to add the given angles and subtract the result from 180°. Therefore, we have:
55°+75° = 130°
⇒ 180°-130° = 50°
Therefore, the measure of the missing angle is 50°.
EXAMPLE 2
Determine the measure of the missing angle in the triangle below.
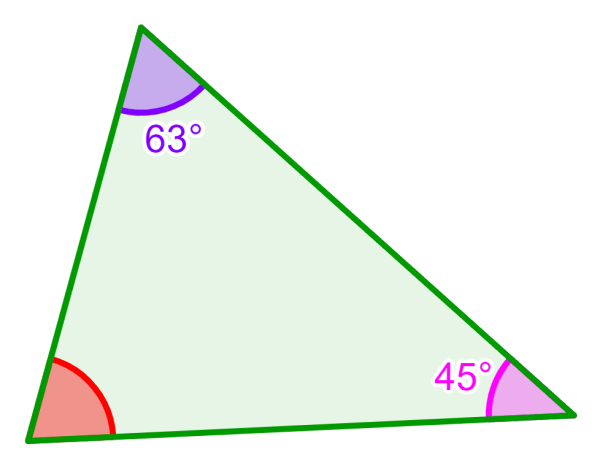
Solution: Similar to the previous example, we add the measures of the given angles and subtract the result from 180°. Therefore, we have:
45°+63° = 108°
⇒ 180°-108° = 72°
Therefore, the measure of the missing angle is 72°.
See also
Interested in learning more about angles of a triangle and other polygons? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
