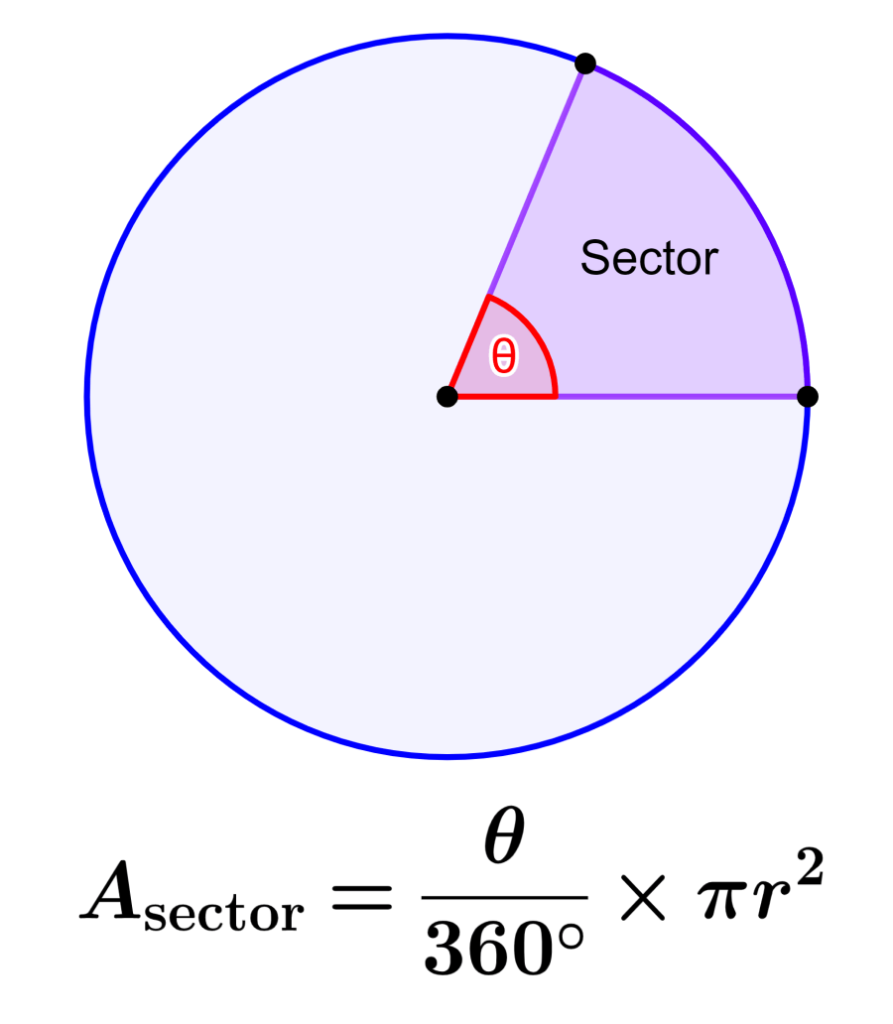
The area of a circular sector represents the amount of space occupied by the sector. We can calculate the area of a circular sector by finding the total area of the circle and multiplying it by the angle of the sector over 360°.
In this article, we will learn how to calculate the area of a given circular sector in both degrees and radians. We will learn about the formulas that we can use, and we will apply them to solve some practice problems.
How to calculate the area of a circular sector?
Let us remember that a circular sector is a portion of the circle that is formed by its two radii and by an arc that joins the radii. A common example of a circular sector is a semicircle, which represents half of a circle.
We can find the area of a circular sector considering that the area will be equal to the total area of the circle multiplied by a fraction that represents the sector with respect to the complete circle.
For example, suppose we want to find the area of the following sector, which represents a quarter of the circle.
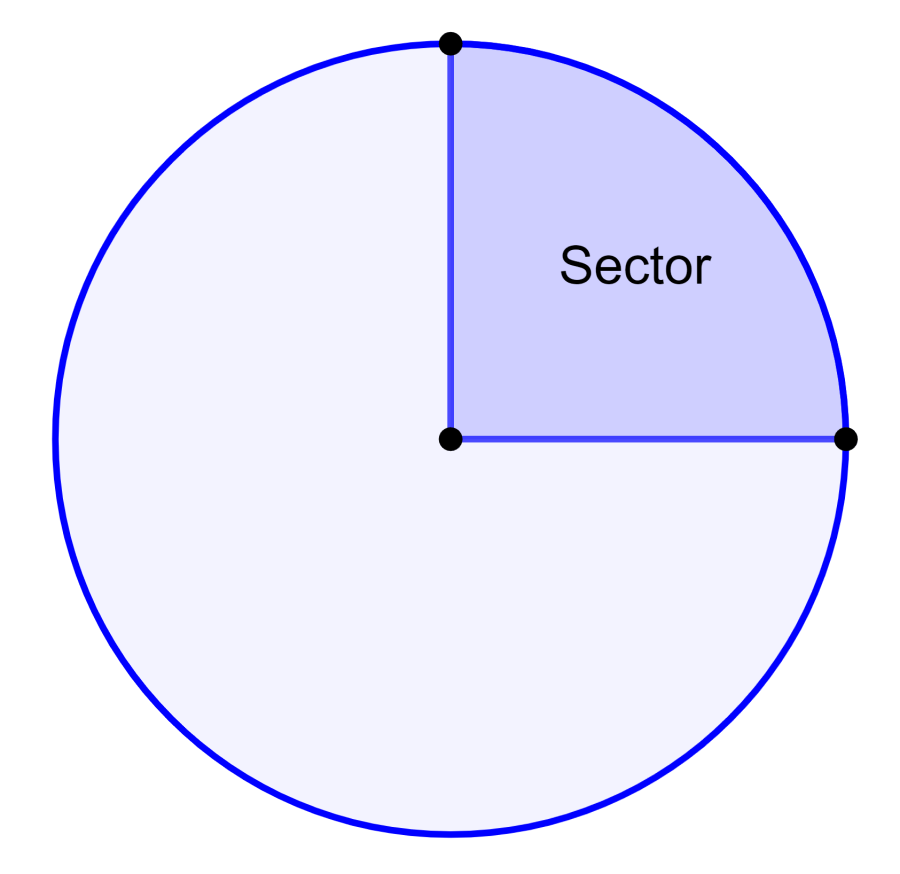
We can start by calculating the area of the circle. Therefore, we see that the radius is equal to 2 units. Using the formula $latex A=\pi r^2$, we get $latex A=50.265$.
Now, we just divide that area by 4 to get the area of the sector. Thus, the area of the sector is equal to 12.566 square units.
This idea can be extended to find the area of any sector using the formulas shown below.
Formulas for the area of a circular sector
We have two main formulas that we can use to find the area of a circular sector depending on how the angle of the circular sector is expressed.
Area of a circular sector using degrees
We know that a complete circle has a total of 360°. In addition, we know that the area of a circle can be found using the formula $latex A=\pi r^2$, where r is the radius of the circle.
Therefore, if we know the angle of the sector, we can find its area with the following formula:
| $$A_{\text{sector}}=\frac{\theta}{360^{\circ}}\times \pi r^2$$ |
where, θ is the angle that represents the given sector in degrees and r is the radius of the circle.
Area of a circular sector using radians
A complete circle has a total of 2π radians, which is equal to 360°. Therefore, we can modify the above formula to use it when we have the circular sector defined in radians.
$$A_{\text{sector}}=\frac{\theta}{360^{\circ}}\times \pi r^2$$
$$A_{\text{sector}}=\frac{\theta}{2\pi}\times \pi r^2$$
| $$A_{\text{sector}}=\frac{\theta}{2}\times r^2$$ |
where, θ is the angle that represents the given sector in radians and r is the radius of the circle.
Area of a circular sector – Examples with answers
Each of the following examples has its respective answer. These problems are solved by applying the formulas for the area of a circular sector.
EXAMPLE 1
Find the area of a circular sector that has a central angle of 30° and a radius of 2 feet.
Solution
In this example, we have a circular sector given in degrees, so we can use the following formula with the given values:
$$A_{\text{sector}}=\frac{\theta}{360^{\circ}}\times \pi r^2$$
$$A_{\text{sector}}=\frac{30^{\circ}}{360^{\circ}}\times \pi (2)^2$$
$$A_{\text{sector}}=\frac{1}{12}\times \pi (4)$$
$$A_{\text{sector}}=\frac{\pi}{3}$$
The area of the sector is $latex \frac{\pi}{3}~ft^2$.
EXAMPLE 2
What is the area of a circular sector that has a radius of 3 inches and a central angle of π/3?
Solution
Since we have a circular sector given in radians, we can use the second formula:
$$A_{\text{sector}}=\frac{\theta}{2}\times r^2$$
$$A_{\text{sector}}=\frac{\frac{\pi}{3}}{2}\times (3)^2$$
$$A_{\text{sector}}=\frac{\pi}{6}\times 9$$
$$A_{\text{sector}}=\frac{3\pi}{2}$$
The area of the circular sector is $latex \frac{3\pi}{2}~in^2$
EXAMPLE 3
If a circular sector has a radius of 4 inches and an angle of 40°, find its area.
Solution
The circular sector is given in degrees, so we use the first formula with the values r=4 and θ=40°. Therefore, we have:
$$A_{\text{sector}}=\frac{\theta}{360^{\circ}}\times \pi r^2$$
$$A_{\text{sector}}=\frac{40^{\circ}}{360^{\circ}}\times \pi (4)^2$$
$$A_{\text{sector}}=\frac{1}{9}\times \pi (16)$$
$$A_{\text{sector}}=5.585$$
The area of the sector is $latex 5.585~in^2$.
EXAMPLE 4
Determine the area of a sector that has an angle of π/4 and a radius of 5 in.
Solution
We are going to use the second formula with the values r=5 and θ=π/4. Therefore, we have:
$$A_{\text{sector}}=\frac{\theta}{2}\times r^2$$
$$A_{\text{sector}}=\frac{\frac{\pi}{4}}{2}\times (5)^2$$
$$A_{\text{sector}}=\frac{\pi}{8}\times 25$$
$$A_{\text{sector}}=9.817$$
The area of the circular sector is $latex 9.817~in^2$
EXAMPLE 5
Find the area of a circular sector that has an angle of 140° and a radius of 2.5 inches.
Solution
Using the first formula with the values r=2.5 and θ=140°, we have:
$$A_{\text{sector}}=\frac{\theta}{360^{\circ}}\times \pi r^2$$
$$A_{\text{sector}}=\frac{140^{\circ}}{360^{\circ}}\times \pi (2.5)^2$$
$$A_{\text{sector}}=\frac{7}{18}\times \pi (6.25)$$
$$A_{\text{sector}}=7.636$$
The area of the sector is $latex 7.636~in^2$.
EXAMPLE 6
Find the area of a circular sector that has an angle of 3π/4 and a radius of 3 ft.
Solution
Using the second formula with the values r=3 and θ=3π/4, we have:
$$A_{\text{sector}}=\frac{\theta}{2}\times r^2$$
$$A_{\text{sector}}=\frac{\frac{3\pi}{4}}{2}\times (3)^2$$
$$A_{\text{sector}}=\frac{3\pi}{8}\times 9$$
$$A_{\text{sector}}=10.603$$
The area of the circular sector is $latex 10.603~ft^2$
EXAMPLE 7
Find the area of a circular sector that has an angle of 110° and a radius of 10 in.
Solution
We use the first formula with the values r=10 and θ=110°, and we have:
$$A_{\text{sector}}=\frac{\theta}{360^{\circ}}\times \pi r^2$$
$$A_{\text{sector}}=\frac{110^{\circ}}{360^{\circ}}\times \pi (10)^2$$
$$A_{\text{sector}}=\frac{11}{36}\times \pi (100)$$
$$A_{\text{sector}}=96$$
The area of the sector is $latex 96~in^2$.
Area of a circular sector – Practice problems
Use the formulas for the area of a circular sector to solve the following practice problems. Click “Check” to verify that your answer is correct.
See also
Interested in learning more about circles? You can visit these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
