The trapezoid rule is a method of approximating the definite integral of a function. It is based on the idea of approximating the area under a curve by a series of trapezoids instead of rectangles, which gives a more accurate estimate.
In this article, we will look at a summary of how to use the trapezoid rule to calculate integrals. In addition, we will solve several practice problems to apply this concept.
How to use the trapezoid rule to solve integrals
To use the trapezoid rule to solve definite integrals, you can follow these steps:
Step 1: Divide the integration interval [a, b] into $latex n$ subintervals of equal width $latex h = \frac{b – a}{n}$.
Step 2: Evaluate the function $latex f(x)$ at the extreme points of each subinterval, i.e., at $latex x = a,$ $latex a + h$, $latex a + 2h$, …, $latex a + (n-1)h$, and $latex b$.
Step 3: Calculate the height of each trapezoid by taking the average of the function values at the extremes of the subinterval, i.e, $latex \frac{f(a) + f(a+h)}{2}$, $latex \frac{f(a+h) + f(a+2h)}{2}$, …, $latex \frac{f(a+(n-1)h) + f(b)}{2}$.
Step 4: Calculate the area of each trapezoid by multiplying the height by the width, that is, $latex \frac{f(a) + f(a+h)}{2} \times h$, $latex \frac{f(a+h) + f(a+2h)}{2} \times h$, …, $latex \frac{f(a+(n-1)h) + f(b)}{2} \times h$.
Step 5: Add the areas of all the trapezoids to obtain the approximation of the definite integral of the function $latex f(x)$ over the interval [a, b].
Alternatively, we can use the following formula:
$$I_a = \frac{\Delta x}{2} ( f(x_0)+2[ f(x_1)+f(x_2)+f(x_3)+f(x_4) ]+f(x_5)$$
The smaller the value of $latex n$, the less accurate the approximation, but using a larger value of $latex n$ will require a longer process.
Therefore, it is important to find a balance between accuracy and efficiency when using the trapezoidal rule for integration.
Trapezoid rule for approximating integrals – Examples with answers
EXAMPLE 1
Find the approximate value, using the trapezium rule, of the following definite integral:
$$ I= \int_{-2}^{2} \exp (-x^{2}) dx $$
Solution
The trapezoid method consists of dividing the integration interval into n subintervals and approximating the area of each one by that of the trapezoid between the abscissa points and the coordinates of the function evaluated at those values.
In this way, the approximate integral $latex I_a$ is obtained by means of the following formula, for the case of $latex n$ regular intervals of width $latex h=\Delta x $.
$$ I_{a}=\frac{1}{2}\Delta x (f(x_{0})+2(f(x_{1})+f(x_{2})+…..+f(x_{n-2})+f(x_{n-1}))+f(x_{n})) $$
We will illustrate the method by choosing 5 subintervals and showing the calculations in detail. It’s clear that if a more accurate result is desired, a larger number of subintervals is necessary.
- $latex f(x)=exp(-x^2)$
- $latex n=5$
- $latex a=-2$
- $latex b=+2$
- $latex h= \Delta x=\frac{b-a}{n} : 0.8$
Then, we have the following values of x:
- $latex x_{0}=a= -2.0$
- $latex x_{1}=a+\frac{1(b-a)}{n}= -1. 2$
- $latex x_{2}=a+\frac{2(b-a)}{n}= -0.4$
- $latex x_{3}=a+\frac{3(b-a)}{n}= 0.4$
- $latex x_{4}=a+\frac{4(b-a)}{n}= 1. 2$
- $latex x_{5}=a+\frac{5(b-a)}{n}= 2.0$
Using these values, we find the values of the function or height of the trapezoids:
- $latex f(x_{0})= 1. 8316×10^{-2}$
- $latex f(x_1)= 0.23693$
- $latex f(x_2)= 0.85214$
- $latex f(x_3)= 0.85214$
- $latex f(x_4)= 0.23693$
- $latex f(x_5)= 1. 8316×10^{-2}$
Finally, we use the following formula:
$$I_a=\frac{h}{2} (f(x_{0})+2(f(x_{1})+f(x_2)+f(x_3)+f(x_4))+f(x_5))= 1. 7572$$
By taking a more precise value of the integral such as: I=1.7642, which was obtained by using many more intervals, we can estimate the error of our 5 sub-interval approximation.
Percentage error: $latex \left( \frac{I-I_a}{I}\right) ×100 =0.40%$
EXAMPLE 2
Use the trapezoid rule to find an approximate value of the following definite integral:
$$I=\int_{0}^{2} \sqrt{x} dx $$
(note: use 5 subintervals)
Solution
We have the following information:
- $latex f(x)=\sqrt{x}$
- $latex n=5$
- $latex a=0$
- $latex b=2$
- $latex \Delta x=\frac{b-a}{n} = 0.4$
Then, we can obtain the following values of x:
- $latex x_0=a= 0.0$
- $latex x_1=a+1\times \Delta x= 0.4$
- $latex x_2=a+2\times \Delta x= 0.8$
- $latex x_3=a+3\times \Delta x= 1. 2$
- $latex x_4=a+4\times \Delta x= 1. 6$
- $latex x_5=a+5\times \Delta x= 2.0$
Using these values, we find the following heights:
- $latex f(x_0)= 0.0$
- $latex f(x_1)= 0.63246$
- $latex f(x_2)= 0.89443$
- $latex f(x_3)= 1. 0954$
- $latex f(x_4)= 1. 2649$
- $latex f(x_5)= 1. 4142$
The approximate value of the integral ($latex I_a$) is obtained by the trapezoid rule formula:
$$I_a = \frac{\Delta x}{2} ( f(x_0)+2[ f(x_1)+f(x_2)+f(x_3)+f(x_4) ]+f(x_5)$$
$$I_a = 1. 84$$
The exact integral is:
$$I=\int_{0}^{2} \sqrt{x} dx = \frac{4}{3} \sqrt{2} = 1.8856 $$
Percentage error: $latex \frac{I-I_a}{I} \times 100 = 2.4% $
EXAMPLE 3
Let f(x) be the function shown in the figure. Find a formula that gives, approximately, the definite integral of this function in the interval [a, b], taking into account that the sum of the area of the trapezoids represented there is numerically close to the value of the area under the curve of the function.
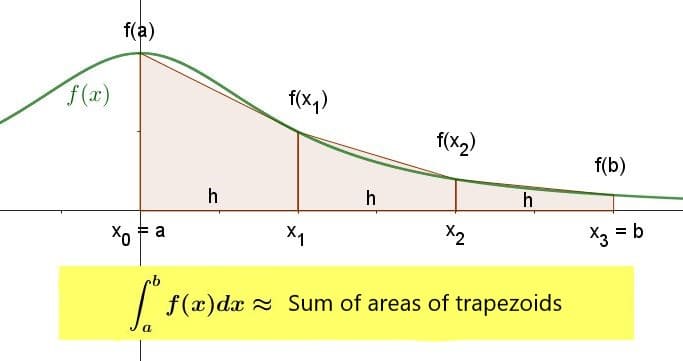
Solution
Let’s start by recalling that a trapezoid is a quadrilateral with two parallel sides, which are called bases. The separation or distance between the two bases of a trapezoid is called the height.
On the other hand, the area of a trapezoid is calculated by multiplying the semi sum (sum divided by 2) of the length of its bases by its height.
In the first trapezoid in the figure above, the length of the larger base is $latex f(a)$ and the length of the smaller base is $latex f(x_1)$. The height is the separation between the bases, that is $latex h$. Then the area of trapezoid 1 is:
$$A_1 = \frac{f(a) + f(x_1)}{2} \cdot h $$
Similarly, the area of trapezoid 2 is given by:
$$A_2 = \frac{f(x_1) + f(x_2)}{2} \cdot h $$
and that of trapezoid 3 is:
$$A_3 = \frac{f(x_2) + f(b)}{2} \cdot h $$
The total area is the sum of the areas of the three trapezoids, which we will call $latex Sum $.
$$ Sum = \frac{f(a) + f(x_1)}{2} \cdot h + \frac{f(x_1) + f(x_2)}{2} \cdot h + \frac{f(x_2) + f(b)}{2} \cdot h $$
We realize that, in this sum, $latex \frac{h}{2} $ is a common factor:
$$ Sum = \frac{h}{2} [f(a) + f(x_1) + f(x_1) + f(x_2) + f(x_2) + f(b)] $$
$$ Sum = \frac{h}{2} [f(a) + 2 \cdot f(x_1) + 2 \cdot f(x_2)] + f(b) $$
$$ Sum = \frac{h}{2} [f(a) + 2 [f(x_1) + f(x_2)] + f(b)] $$
That is, the value of the definite integral can be approximated, in the case n=3, by:
$$ \int_a^b f(x) dx \approx \frac{h}{2} [f(x_0) + 2 [f(x_1) + f(x_2)] + f(x_3)] $$
EXAMPLE 4
The figure below shows the graph of the function $latex f(x)= \frac{1}{1+x^2}$. Find, with the data in the figure, the approximate value of the definite integral:
$$ \int_0^3 \frac{1}{1+x^2} dx $$
Compare the result obtained with that of the exact value and estimate the percentage error of the approximation.
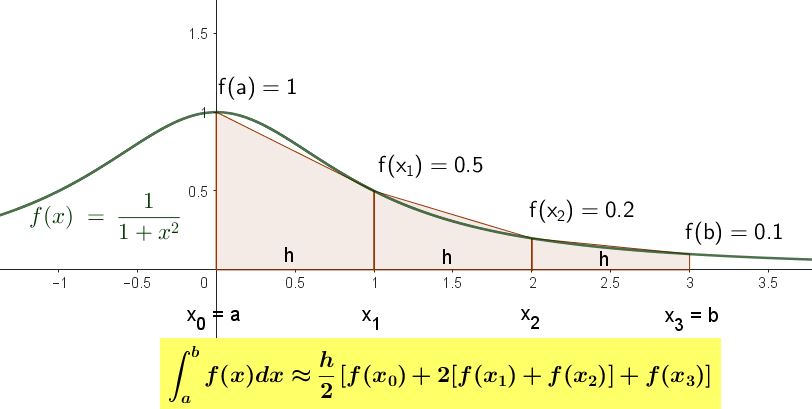
Solution
An approximation to the given definite integral will be found by using the formula for the rule of trapezoids for the case of three subintervals, i.e. n=3.
$$ \int_a^b f(x) dx \approx \frac{h}{2} [f(x_0) + 2 [f(x_1) + f(x_2)] + f(x_3)] $$
Substituting the given values, we have:
$$ \int_0^3 \frac{1}{1+x^2} dx \approx \frac{1}{2} [1 + 2 [0.5 + 0.2] + 0.1] = 1.25 $$
This integral can be calculated in exact analytical form:
$$ \int_0^3 \frac{1}{1+x^2} dx = \left |Arctan(x) \right |_0^3 = Arctan(3)-Arctan(0) = 1.24905 $$
The percentage error of our approximation is:
$$ \frac{1.25-1.24905}{1.24905} \times 100 = 0.08 \% $$
This shows that if the function has smooth variation in the integration interval, accurate results can be achieved with the trapezoid rule, even taking a few subintervals.
EXAMPLE 5
Find an approximate solution to the integral:
$$ \int_0^{\pi /2} cos^3(x) dx $$
applying the trapezoid rule and taking four subdivisions, i.e. n=4.
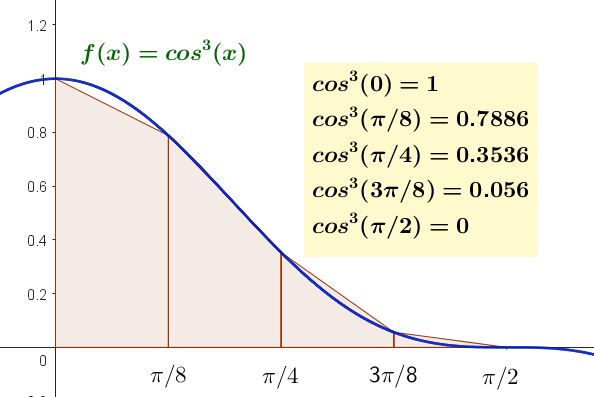
Solution
The formula for the rule of trapezoids for the case of four subintervals (n=4) is:
$$ \int_0^{\pi /4} f(x) dx \approx \frac{h}{2} [f(x_0) + 2 [f(x_1) + f(x_2)+f(x_3)] + f(x_4)] $$
The values of the function $latex f(x)=cos^3(x)$ at the extremes of the subintervals are shown in the figure above:
$$ \int_0^{\pi /4} f(x) dx \approx \frac{\pi /8}{2} [1 + 2 [0.7886 + 0.3536 + 0.056] + 0.0] = 0.6669 $$
The exact result of this integral is: 2/3= 0.66667
The percentage error of the approximation is:
$$ \frac{0.6669-0.66667}{0.66667} \times 100 = 0.03 \% $$
EXAMPLE 6
Find the value of the indicated integral
$$ \int_0^{\pi /4} sec(x) dx $$
using the trapezoid rule and taking three subdivisions, i.e. n=3.
Solution
Sketching a graph of the function and dividing it into three trapezoids, we obtain the following:

Then, we use the formula for the trapezoid rule to find the value of the integral:
$$ I_a = \frac{\pi /12}{2} [sec(0) + 2 [sec( \pi /12) + sec( \pi /6))] + sec( \pi /4)]=0.889 $$
EXAMPLE 7
By means of the sum of the areas of trapezoids, find an approximate value of the indicated integral
$$ \int_{-4}^{+4} \frac{4}{2+x^4} dx $$
Use nine subdivisions (n=9). Present the operations in a table.
Solution
The formula for the trapezoid rule will be used:
$$ I_a=\frac{h}{2} (f(x_{0})+2(f(x_{1})+f(x_{2})+…..+f(x_{n-2})+f(x_{n-1}))+f(x_{n})) $$
with n=9 and the function $latex \frac{4}{2+x^4} $.
The intermediate calculations and the final result (highlighted in green) are shown in the following table:
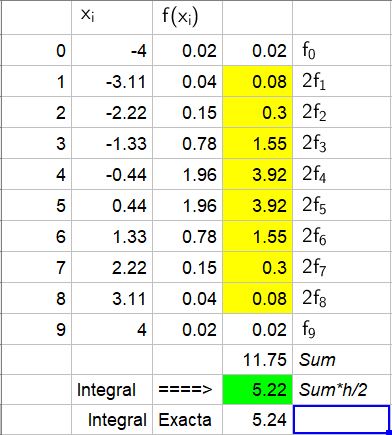
The value obtained by the trapezoidal approximation is 5.22, while the exact value is 5.24.
EXAMPLE 8
Apply the trapezoid rule to find a quadrature (definite integral) of the following function, in the interval [-4, 4]:
$$ f(x) = \frac{2}{\sqrt{1+x^2}} $$.
Note: Use n=8 and show the results of the operations in a table.
Solution
The value of h is: $latex h= \frac{b-a}{n}= \frac{4-(-4)}{8}=1$.
Then, we obtain the 8 values of x and their corresponding function values. Then, we use the formula for the trapezoid rule:

The value of the integral is 8.37.
EXAMPLE 9
Using the trapezoid rule find an approximation to the definite integral of the following function, in the interval [-4, 4]:
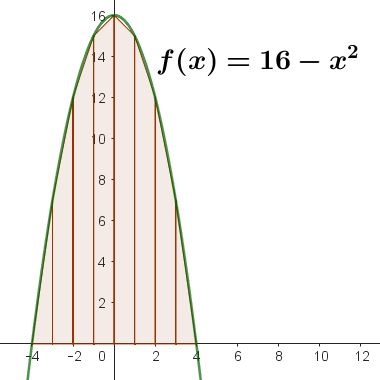
Note: Use n=8 and show the results of the operations in a table.
Solution
The distance between the lower limit $latex x=-4$ and the upper limit $latex x=4$ is 8, so dividing by the 8 intervals, we have $latex h=1$.
Then, we determine the values of x and their corresponding “heights”, and then use the trapezoid rule:
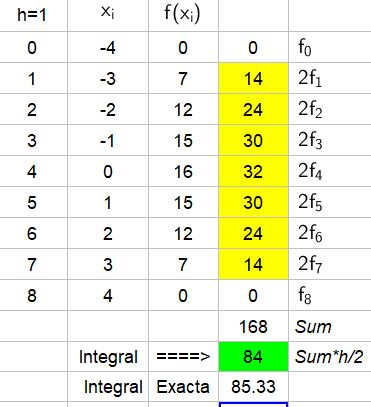
EXAMPLE 10
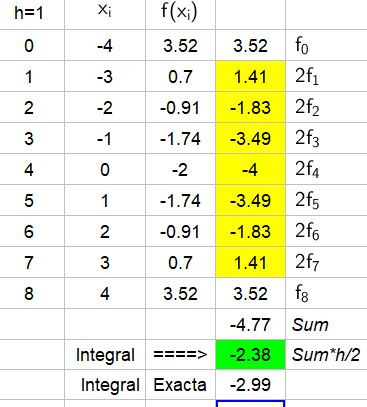
Find the definite integral between -4 and 4, by sum of trapezoids approximation for the function shown. Incidentally, this is the function that describes a rope or chain hanging between two fixed points, which is why it is known as a catenary.

Note: Use n=8 and show the results of the operations in a table.
Solution
Similar to the previous example, the value of $latex h$ is 1, since the distance between the limits of integration is 8 and we have 8 intervals.
The following table shows the values of x, their corresponding f values, and the result of applying the trapezoid rule:
Trapezoid rule – Practice problems


Use the trapezoid rule with 4 subintervals or trapezoids to find an approximate value for:$$\int_{1}^{9}\sqrt{\ln(x)}dx$$
Write the answer to two decimal places.
See also
Interested in learning more about numerical methods? You can take a look at these pages:



