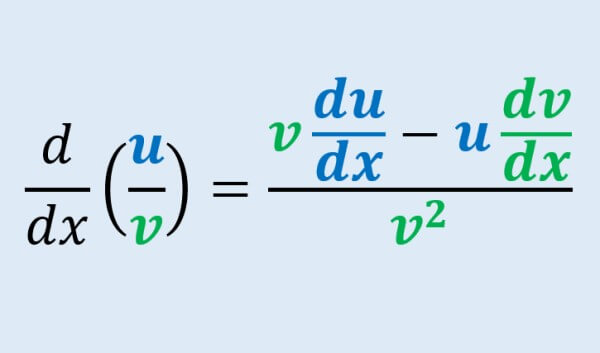Derivation exercises that involve the quotient of functions can be solved using the quotient rule formula. This formula allows us to derive a quotient of functions such as but not limited to $latex \frac{f}{g} (x) = \frac{f(x)}{g(x)}$.
Here, we will look at the summary of the quotient rule. Additionally, we will explore several examples with answers to understand the application of the quotient rule formula.
Summary of the quotient rule
The quotient rule is a very useful formula for deriving quotients of functions. It is a rule that states that the derivative of a quotient of two functions is equal to the function in the denominator g(x) multiplied by the derivative of the numerator f(x) subtracted from the numerator f(x) multiplied by the derivative of the denominator g(x), all divided by the square of the denominator g(x).
This gives us the formula for the quotient rule as:
$$\left(\frac{f}{g}\right)'(x) = \frac{g(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} f'(x) \hspace{2.3 pt} – \hspace{2.3 pt} f(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} g'(x)}{( \hspace{1.15 pt} g(x) \hspace{1.15 pt} )^2}$$
or in a shorter form, it can be illustrated as:
$$\frac{d}{dx}\left(\frac{u}{v}\right) = \frac{vu’ \hspace{2.3 pt} – \hspace{2.3 pt} uv’}{v^2}$$
where $latex u = f(x)$ is the numerator/dividend of the given problem and $latex v = g(x)$ is the denominator/divisor of the given problem.
You can use either of these two forms of the product rule formula according to your preference.
We use this formula to derive functions that have the following form:
$$\frac{f}{g}(x) = \frac{f(x)}{g(x)}$$
or
$$F(x) = \frac{u}{v}$$
where $latex f(x)$ or $latex u$ is the numerator/divider while $latex g(x)$ and $latex v$ is the denominator/divisor of the given problem.
Quotient rule – Examples with answers
EXAMPLE 1
Derive the following:
$$f(x) = \frac{x^3}{x-5}$$
Solution
We have $latex x^3$ as numerator/dividend and $latex x-5$ as denominator/divisor.
Based on the quotient rule formula, $latex u$ is the numerator and $latex v$ is the denominator. Therefore, we have
$latex u = x^3$
$latex v = x-5$
$latex f(x) = \frac{u}{v}$
Then, we derive $latex u$ and $latex v$ individually and then substitute by the quotient rule formula below:
$latex u = x^3$
$latex u’ = 3x^2$
$latex v = x-5$
$latex v’ = 1$
Substituting $latex u$, $latex v$, $latex u’$ and $latex v’$ into the quotient rule formula, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(x-5) \cdot (3x^2) – (x^3) \cdot (1)}{(x-5)^2}$$
Simplifying algebraically, we get
$$f'(x) = \frac{(3x^3 – 15x^2) – (x^3)}{(x^2-10x+25)}$$
And the final answer is:
$$f'(x) = \frac{2x^3 – 15x^2}{x^2-10x+25}$$
EXAMPLE 2
What is the derivative of the following?
$$f(x) = \frac{6x^3}{\ln{(x)}}$$
Solution
Based on the given, we have $latex 6x^3$ as the numerator/dividend and $latex \ln{(x)}$ as the denominator/divisor. Therefore, we have
$latex u = 6x^3$
$latex v = \ln{(x)}$
$latex f(x) = \frac{u}{v}$
Next, we derive $latex u$ and $latex v$ individually:
$latex u = 6x^3$
$latex u’ = 18x^2$
$latex v = \ln{(x)}$
$latex v’ = \frac{1}{x}$
Substituting $latex u$, $latex v$, $latex u’$ and $latex v’$ into the quotient rule formula, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(\ln{(x)}) \cdot (18x^2) – (6x^3) \cdot (\frac{1}{x})}{(\ln{(x)})^2}$$
Simplifying, we obtain
$$f'(x) = \frac{18x^2 \ln{(x)} – \frac{6x^3}{x}}{(\ln{(x)})^2}$$
And the final answer is:
$$f'(x) = \frac{18x^2 \ln{(x)} – 6x^2}{(\ln{(x)})^2}$$
EXAMPLE 3
Derive the following function:
$$f(x) = \frac{5x^5-x^4}{30x-12x^2}$$
Solution
$latex u$ is the numerator and $latex v$ is the denominator. Therefore, we have
$latex u = 5x^5-x^4$
$latex v = 30x-12x^2$
$latex f(x) = \frac{u}{v}$
Then, we derive $latex u$ and $latex v$ individually and then substitute by the quotient rule formula below:
$latex u = 5x^5-x^4$
$latex u’ = 25x^4-4x^3$
$latex v = 30x-12x^2$
$latex v’ = 30-24x$
Using the quotient rule, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(30x-12x^2) \cdot (25x^4-4x^3) – (5x^5-x^4) \cdot (30-24x)}{(30x-12x^2)^2}$$
Simplifying, we obtain
$$f'(x) = \frac{(-300x^6+798x^5-120x^4) – (-120x^6+174x^5-30x^4)}{9x^4-72x^3+144x^2}$$
$$f'(x) = \frac{-180x^6+624x^5-90x^4}{9x^4-72x^3+144x^2}$$
$$f'(x) = \frac{-(180x^6-624x^5+90x^4)}{9x^4-72x^3+144x^2}$$
And the final answer is:
$$f'(x) = -\frac{180x^6-624x^5+90x^4}{9x^4-72x^3+144x^2}$$
EXAMPLE 4
Find the derivative of the following function:
$$f(x) = \frac{x^2}{e^{2x}}$$
Solution
Based on the given, we have $latex u=x^2$ as numerator/dividend and $latex v=e^{(2x)}$ as denominator/divisor. Therefore, we have
$latex u = x^2$
$latex v = e^{2x}$
$latex f(x) = \frac{u}{v}$
The derivatives of $latex u$ and $latex v$ are:
$latex u = x^2$
$latex u’ = 2x$
$latex v = e^{2x}$
$latex v’ = 2e^{2x}$
Substituting $latex u$, $latex v$, $latex u’$ and $latex v’$ into the quotient rule formula, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(e^{2x}) \cdot (2x) – (x^2) \cdot (2e^{2x})}{(e^{2x})^2}$$
Simplifying, we have:
$$f'(x) = \frac{(2xe^{2x}) – (2x^2 e^{2x})}{(e^{2x})^2}$$
$$f'(x) = \frac{2xe^{2x}}{(e^{2x})^2} – \frac{2x^2 e^{2x}}{(e^{2x})^2}$$
$$f'(x) = \frac{2x}{e^{2x}} – \frac{2x^2}{e^{2x}}$$
And the final answer is:
$$f'(x) = \frac{2x – 2x^2}{e^{2x}}$$
EXAMPLE 5
What is the derivative of f(x)?
$$f(x) = \frac{\sin{(x)}}{\tan{(x)}}$$
Solution
$latex u$ is the numerator and $latex v$ is the denominator. Therefore, we have
$latex u = \sin{(x)}$
$latex v =\tan{(x)}$
$latex f(x) = \frac{u}{v}$
Next, we derive $latex u$ and $latex v$ individually:
$latex u = \sin{(x)}$
$latex u’ = \cos{(x)}$
$latex v=\tan{(x)}$
$latex v’ = \sec^{2}{(x)}$
Now, we can use the quotient rule formula to derive our given problem:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(\sin{(x)}) \cdot (\sec^{2}{(x)}) – (\tan{(x)}) \cdot (\cos{(x)})}{(\tan{(x)})^2}$$
Simplifying algebraically and applying trigonometric identities, we get
$$\frac{d}{dx}f(x) = \frac{(\sin{(x)}) \cdot (\frac{1}{cos^{2}{(x)}}) – (\frac{\sin{(x)}}{\cos{(x)}}) \cdot (\cos{(x)})}{\tan^{2}{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{(\frac{\sin{(x)}}{\cos{(x)}}) \cdot (\frac{1}{cos{(x)}}) – (\sin{(x)}}{\tan^{2}{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{\tan{(x)} \cdot \sec{(x)} – \sin{(x)}}{\tan^{2}{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{\tan{(x)} \sec{(x)}}{\tan^{2}{(x)}} – \frac{\sin{(x)}}{\tan^{2}{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{\tan{(x)} \sec{(x)}}{\tan^{2}{(x)}} – \frac{\sin{(x)}}{(\frac{\sin{(x)}}{\cos{(x)}})^2}$$
$$\frac{d}{dx}f(x) = \frac{sec{(x)}}{\tan{(x)}} – \frac{\sin{(x)} \cos^{2}{(x)}}{\sin^{2}{(x)}}$$
$$\frac{d}{dx}f(x) = \left[\frac{\frac{1}{\cos{(x)}}}{\frac{\cos{(x)}}{\sin{(x)}}}\right] – \left[\sin{(x)} \cdot \frac{cos^{2}{(x)}}{sin^{2}{(x)}}\right]$$
$$\frac{d}{dx}f(x) = \frac{\cos{(x)}}{\cos{(x)} \cdot \sin{(x)}} – \frac{cos^{2}{(x)}}{sin{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{1}{\sin{(x)}} – \frac{\sin^{2}{(x)}-1}{sin{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{1 – \sin^{2}{(x)} – 1}{sin{(x)}}$$
$$\frac{d}{dx}f(x) = \frac{-\sin^{2}{(x)}}{sin{(x)}}$$
And the final answer is:
$latex f'(x) = -sin{(x)}$
EXAMPLE 6
Derive the function f(x):
$$f(x) = \frac{\sqrt[5]{x^3}}{x^5+3x^2-4x}$$
Solution
Based on the given, we have $latex u=\sqrt[5]{x^3}$ as the numerator/dividend and $latex v=x^5+3x^2-4x$ as the denominator/divisor.
$latex u = \sqrt[5]{x^3}=x^{\frac{3}{5}}$
$latex v = x^5+3x^2-4x$
$latex f(x) = \frac{u}{v}$
Next, let us derive $latex u$ and $latex v$ individually and then substitute by the quotient rule formula below:
$$u = x^{\frac{3}{5}}$$
$$ u’ = \frac{3}{5} x^{-\frac{2}{5}}$$
$latex v = x^5+3x^2-4x$
$latex v’ = 5x^4+6x-4$
Now, we can use the quotient rule formula to derive our given problem:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(x^5+3x^2-4x) \cdot \left( \frac{3}{5} x^{-\frac{2}{5}} \right) – \left(x^{\frac{3}{5}} \right) \cdot (5x^4+6x-4)}{(x^5+3x^2-4x)^2}$$
Simplifying, we have:
$$\frac{d}{dx}f(x) = \frac{\left( \frac{3}{5} x^{\frac{23}{5}}+\frac{9}{5} x^{\frac{8}{5}}-\frac{12}{5} x^{\frac{3}{5}} \right) – \left( 5x^{\frac{23}{5}}+6x^{\frac{8}{5}}-4x^{\frac{3}{5}} \right)}{(x^5+3x^2-4x)^2}$$
$$\frac{d}{dx}f(x) = \frac{\frac{22}{5} x^{\frac{23}{5}}-\frac{21}{5} x^{\frac{8}{5}}+\frac{8}{5} x^{\frac{3}{5}}}{(x^5+3x^2-4x)^2}$$
$$\frac{d}{dx}f(x) = \frac{\frac{-22 x^{\frac{23}{5}} – 21 x^{\frac{8}{5}} + 8 x^{\frac{3}{5}}}{5}}{(x^5+3x^2-4x)^2}$$
And the final answer is:
$$f'(x) = \frac{8 \sqrt[5]{x^3} -22 \sqrt[5]{x^{23}} – 21 \sqrt[5]{x^8}}{5(x^5+3x^2-4x)^2}$$
in radical form
EXAMPLE 7
What is the derivative of the given function?
$$f(x) = \frac{\ln{(x)}}{\cos{(x)}}$$
Solution
In this case, we have:
$latex u = \ln{(x)}$
$latex v = \cos{(x)}$
$latex f(x) = \frac{u}{v}$
Then, let us derive $latex u$ and $latex v$ individually:
$latex u = \ln{(x)}$
$latex u’ = \frac{1}{x}$
$latex v = \cos{(x)}$
$latex v’ = -\sin{(x)}$
After doing this, we can use the quotient rule formula to derive our given problem:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) = \frac{(\cos{(x)}) \cdot (\frac{1}{x}) – (\ln{(x)}) \cdot (-\sin{(x)})}{(\cos{(x)})^2}$$
Simplifying the obtained expression, we have:
$$f'(x) = \frac{(\frac{\cos{(x)}}{x}) – (-\sin{(x)} \ln{(x)})}{(\cos{(x)})^2}$$
$$f'(x) = \frac{\frac{\cos{(x)}}{x}) + \sin{(x)} \ln{(x)}}{(\cos{(x)})^2}$$
$$f'(x) = \frac{\frac{\cos{(x)}}{x}) + \frac{x \sin{(x)} \ln{(x)}}{x}}{\cos^{2}{(x)}}$$
And the final answer is:
$$f'(x) = \frac{\cos{(x)} + x \sin{(x)} \ln{(x)} }{x \cos^{2}{(x)}}$$
EXAMPLE 8
Find the derivative of the given function:
$$f(x) = \frac{x^3}{\sin^{2}{(x)}}$$
Solution
$latex u$ is the numerator and $latex v$ is the denominator, so we have
$latex u = x^3$
$latex v = \sin^{2}{(x)}$
$latex f(x) = \frac{u}{v}$
Now, let’s derive $latex u$ and $latex v$ individually and then substitute by the quotient rule formula below:
$latex u = x^3$
$latex u’ = 3x^2$
$latex v = \sin^{2}{(x)}$
$latex v’ = 2 \sin{(x)} \cos{(x)}$
Substituting $latex u$, $latex v$, $latex u’$ and $latex v’$ into the quotient rule formula, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$ \frac{d}{dx}f(x) = \frac{(\sin^{2}{(x)}) \cdot (3x^2) – (x^3) \cdot (2 \sin{(x)} \cos{(x)})}{(\sin^{2}{(x)})^2}$$
Simplifying algebraically and applying some trigonometric identities, we get
$$f'(x) = \frac{(3x^2 \sin^{2}{(x)}) – (2x^3 \sin{(x)} \cos{(x)})}{\sin^{4}{(x)}}$$
$$f'(x) = \frac{3x^2 \sin^{2}{(x)}}{\sin^{4}{(x)}} – \frac{2x^3 \sin{(x)} \cos{(x)}}{\sin^{4}{(x)}}$$
$$f'(x) = \frac{3x^2}{\sin^{2}{(x)}} – \frac{2x^3 \cos{(x)}}{\sin^{3}{(x)}}$$
$$f'(x) = 3x^2 \csc^{2}{(x)} – 2x^3 \cdot \frac{\cos{(x)}}{\sin{(x)}} \cdot \frac{1}{\sin^{2}{(x)}}$$
And the final answer is:
$$f'(x) = 3x^2 \csc^{2}{(x)} – 2x^3 \cot{(x)} \csc^{2}{(x)}$$
EXAMPLE 9
What is the derivative of the following function?
$$f(x) = \frac{5x^x}{\cos{(3x)}}$$
Solution
We can observe the following:
$latex u = 5x^x$
$latex v = \cos{(3x)}$
$latex f(x) = \frac{u}{v}$
Finding the derivatives of $latex u$ and $latex v$, we have:
$latex u = 5x^x$
$latex u’ = 5x^x \ln{(x)} + 5x^x$
$latex v = \cos{(3x)}$
$latex v’ = -3 \sin{(3x)}$
Substituting $latex u$, $latex v$, $latex u’$ and $latex v’$ into the quotient rule formula, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) =\frac{(\cos{(3x)}) \cdot (5x^x \ln{(x)} + 5x^x) – (5x^x) \cdot (-3 \sin{(3x)})}{(\cos{(3x)})^2}$$
Simplifying algebraically and applying some trigonometric identities, we get
$$f'(x) =\frac{(5x^x \cos{(3x)} \ln{(x)} + 5x^x \cos{(3x)}) – (-15x^x \sin{(3x)})}{\cos^{2}{(3x)}}$$
$$f'(x) =\frac{5x^x \cos{(3x)} \ln{(x)} + 5x^x \cos{(3x)} + 15x^x \sin{(3x)}}{\cos^{2}{(3x)}}$$
$$f'(x) = \frac{5x^x \cos{(3x)} \ln{(x)}}{\cos^{2}{(3x)}}+ \frac{5x^x \cos{(3x)}}{\cos^{2}{(3x)}} + \frac{15x^x \sin{(3x)}}{\cos^{2}{(3x)}}$$
$$ f'(x) = 5x^x \ln{(x)} \cdot \frac{1}{\cos{(3x)}}+ 5x^x \cdot \frac{1}{\cos{(3x)}} + 15x^x \cdot \frac{\sin{(3x)}}{\cos{(3x)}} \cdot \frac{1}{\cos{(3x)}}$$
And the final answer is:
$$f'(x) = 5x^x \ln{(x)} \sec{(3x)} + 5x^x \sec{(3x)}+ 15x^x \sec{(3x)} \tan{(3x)}$$
EXAMPLE 10
Find the derivative of the given function:
$$f'(x) = \frac{x^{e^x}}{e^{\sin{(x)}}}$$
Solution
We have $latex x^{e^x}$ as the numerator/dividend and $latex e^{\sin{(x)}}$ as the denominator/divisor. Therefore, we have
$latex u = x^{e^x}$
$latex v = e^{\sin{(x)}}$
$latex f(x) = \frac{u}{v}$
Next, let’s derive $latex u$ and $latex v$ individually and then substitute by the quotient rule formula below:
$latex u = x^{e^x}$
$latex u’ = x^{e^x} e^x \ln{(x)} + \frac{x^{e^x} e^x}{x}$
$latex v = e^{\sin{(x)}}$
$latex v’ = e^{\sin{(x)}} \cos{(x)}$
Substituting $latex u$, $latex v$, $latex u’$ and $latex v’$ into the quotient rule formula, we have:
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’-uv’}{v^2}$$
$$\frac{d}{dx}f(x) =\frac{(e^{\sin{(x)}}) \cdot (x^{e^x} e^x \ln{(x)} + \frac{x^{e^x} e^x}{x}) – (x^{e^x}) \cdot (e^{\sin{(x)}} \cos{(x)})}{(e^{\sin{(x)}})^2}$$
Simplifying algebraically and applying some trigonometric identities, we get
$$ \frac{d}{dx}f(x) = \frac{(e^{\sin{(x)}}) \cdot (x^{e^x} e^x \ln{(x)} + \frac{x^{e^x} e^x}{x})}{(e^{\sin{(x)}})^2}– \frac{(x^{e^x}) \cdot (e^{\sin{(x)}} \cos{(x)})}{(e^{\sin{(x)}})^2}$$
$$ \frac{d}{dx}f(x) = \frac{\frac{x^{e^x} (xe^x \ln{(x)} + e^x)}{x} – x^{e^x} \cos{(x)}}{e^{\sin{(x)}}}$$
$$\frac{d}{dx}f(x) = \frac{\frac{x^{e^x} (xe^x \ln{(x)} + e^x) – x^{e^x} (x \cos{(x)})}{x}}{e^{\sin{(x)}}}$$
$$f'(x) = \frac{x^{e^x} (xe^x \ln{(x)} + e^x) – x^{e^x} (x \cos{(x)})}{xe^{\sin{(x)}}}$$
And the final answer is:
$$f'(x) = \frac{x^{e^x} \left[ (e^x (x \ln{(x)} + 1)) – x \cos{(x)} \right]}{xe^{\sin{(x)}}}$$
Quotient rule – Practice problems


Find the derivative of the following function and determine the value of $latex f^{\prime}(1)$. $$f(x) = \left( \frac{x-3}{\sqrt{x}} \right)^2$$
Write the answer in the input box
See also
Interested in learning more about the quotient rule? Check out these pages: