The function y=ex is called the exponential function. The derivative of the exponential function ex is equal to ex. This also means that the integral of ex is ex. Compound exponential functions can be differentiated with the chain rule.
Here, we will learn why the derivative of ex is ex. Also, we will learn how to find the derivative of compound exponential functions with some examples.
CALCULUS
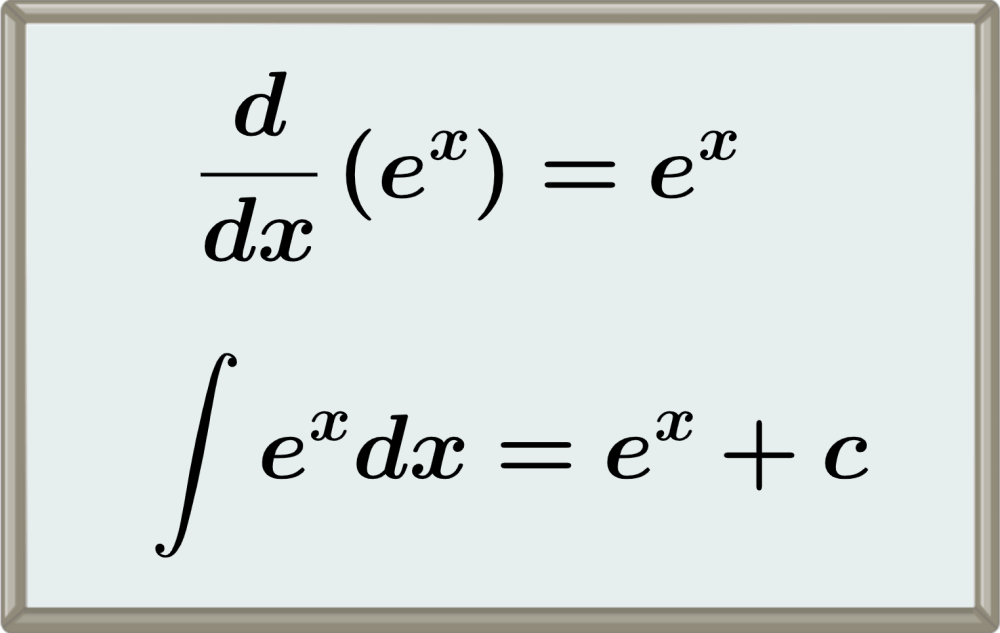
Relevant for…
Learning about derivatives and integrals of exponential functions.
CALCULUS
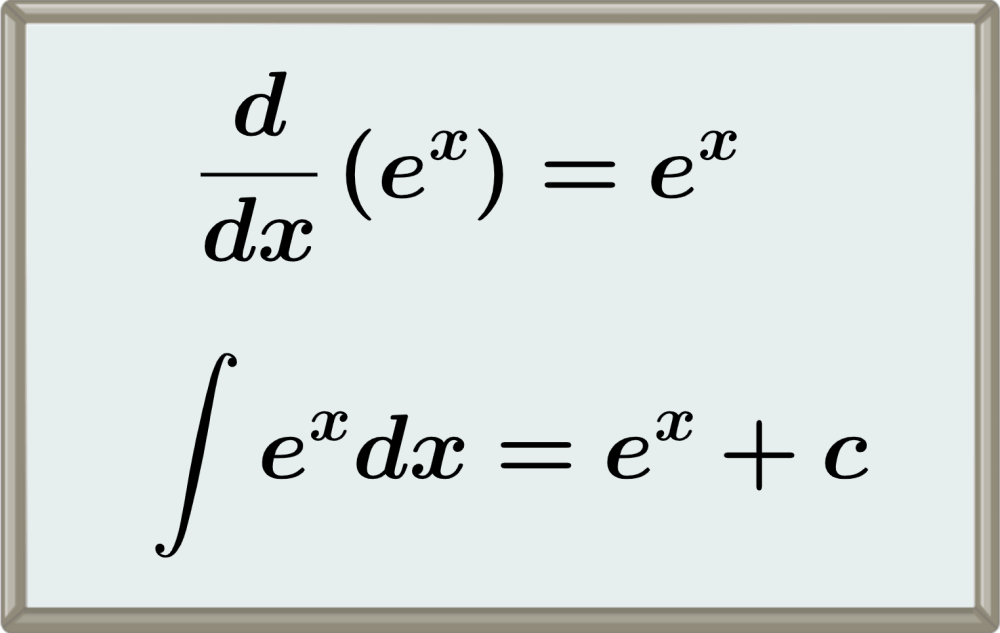
Relevant for…
Learning about derivatives and integrals of exponential functions.
Why ex is the derivative of ex?
The derivative of the exponential function ex is ex because the slope of the curve ex is equal to ex.
We can visualize this idea by considering the graph of the function $latex y=2^x$ shown below:
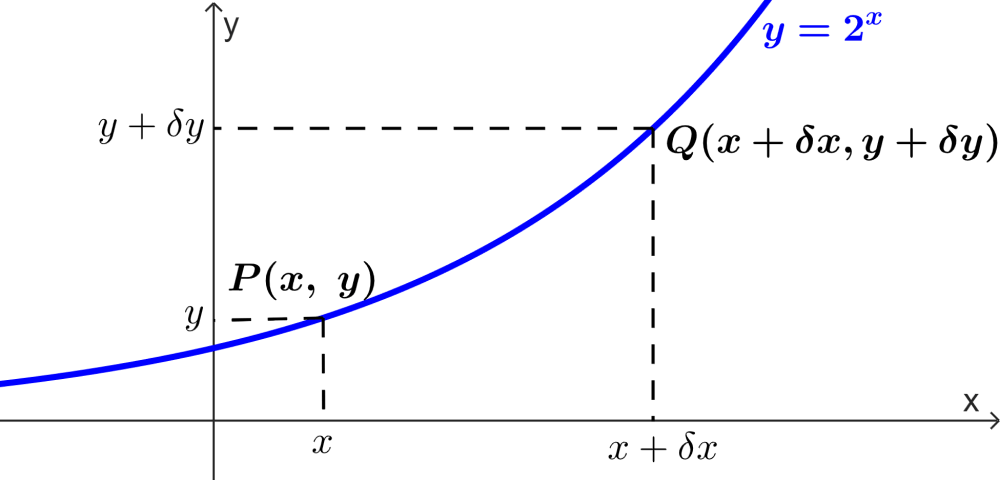
The points $latex P(x,~y)$ and $latex Q(x+\delta x,~y+\delta y)$ are two close points that lie on the curve $latex y=2^x$. Then, we have:
$latex y+\delta y=2^{x+\delta x}$
$latex \delta y=2^{x+\delta x}-y$
$latex =2^{x+\delta x}-2^x$
$latex \delta y=2^x(2^{\delta x}-1)$
If we divide both sides of this equation by $latex \delta x$, we have:
$$\frac{\delta y}{\delta x}=2^x\left(\frac{2^{\delta x}-1}{\delta x}\right)$$
Considering that $latex \frac{dy}{dx}=\lim_{\delta x \to 0}\left[\frac{\delta y}{\delta x}\right]$, we have:
$$\frac{dy}{dx}=\lim_{\delta x \to 0}\left[ 2^x\left(\frac{2^{\delta x}-1}{\delta x}\right)\right]$$
$$=2^x \times \lim_{\delta x \to 0}\left(\frac{2^{\delta x}-1}{\delta x}\right)$$
Taking very small values of $latex \delta x$ and using a calculator, we have:
$$\lim_{\delta x \to 0}\left(\frac{2^{\delta x}-1}{\delta x}\right)\approx 0.693$$
This means that the derivative of $latex 2^x$ is:
$$\dfrac{d}{dx}(2^x)\approx 0.693 \times 2^x$$
If we do the same for $latex 3^x$, we have:
$$\frac{d}{dx}(3^x)=3^x \times \lim_{\delta x \to 0}\left(\frac{3^{\delta x}-1}{\delta x}\right)$$
Taking very small values of $latex \delta x$ and using a calculator, we have:
$$\lim_{\delta x \to 0}\left(\frac{3^{\delta x}-1}{\delta x}\right)\approx 1.099$$
$$\dfrac{d}{dx}(3^x)\approx 1.099 \times 3^x$$
We can observe that for $latex y=2^x$, the slope of the curve ($latex \frac{dy}{dx}$) is less than $latex y=2^x$ and in the case of $latex y=3^x$, the slope is greater than $latex y=3^x$.
There exists an exponential function $latex y=a^x$ in which its slope is equal to $latex y=a^x$. This value is $latex a=2.71828$ and is denoted by the symbol $latex e$.
Derivatives and integrals of exponential functions – Examples with answers
EXAMPLE 1
Find the derivative of the function $latex y=e^{3x}$.
Solution
We know that the derivative of the function $latex y=e^x$ is $latex \frac{dy}{dx}=e^x$.
Then, we use the chain rule to derive:
$$\frac{dy}{dx}=e^{2x}(2x)^{\prime}$$
$$\frac{dy}{dx}=2 e^{2x}$$
EXAMPLE 2
What is the derivative of the function $latex y=5e^{\frac{1}{x}}$?
Solution
Using the chain rule, we have:
$$\frac{dy}{dx}=5e^{\frac{1}{x}}\left(\frac{1}{x}\right)^{\prime}$$
$$=5e^{\frac{1}{x}}\left(-\frac{1}{x^2}\right)$$
$$\frac{dy}{dx}=-\frac{5}{x^2}e^{\frac{1}{x}}$$
EXAMPLE 3
Find the derivative of the following function:
$$y=\frac{2}{3+e^{3x}}$$
Solution
We can write the function as follows:
$latex y=2(3+e^{3x})^{-1}$
Now, we use the chain rule:
$$\dfrac{dy}{dx}=-2(3+e^{3x})^{-2}(3+e^{3x})^{\prime}$$
$$=-2(3+e^{3x})^{-2}(3e^{3x})$$
$$\dfrac{dy}{dx}=\frac{-6e^{3x}}{(3+e^{3x})^2}$$
EXAMPLE 4
Solve the following integral:
$$\int 2e^{-x} dx$$
Solution
To solve this integral, we observe that the derivative of $latex e^{-x}$ is $latex -e^{-x}$. Then, we have:
$$\int 2e^{-x} dx =-2e^{-x}+c$$
EXAMPLE 5
Find the result of the following integral:
$$\int (1-e^{-3x})^2 dx$$
Solution
We can start by expanding the parenthesis expression to get:
$$\int (1-e^{-3x})^2 dx = \int (1-2e^{-3x}+e^{-6x}) dx$$
Then, we have:
$$\int (1-e^{-3x})^2 dx = x+\frac{2}{3}e^{-3x}-\frac{e^{-6x}}{6}+c$$
EXAMPLE 6
Find the derivative of the following function:
$latex y=x^2e^x$
Solution
In this case, we can use the rule of the product of derivatives and we have:
$$\dfrac{dy}{dx}=x^2(e^x)^{\prime}+e^x(x^2)^{\prime}$$
$$=x^2e^x+2xe^x$$
$$\dfrac{dy}{dx}=xe^x(x+2)$$
Derivatives and integrals of exponential functions – Practice problems
See also
Interested in learning more about derivatives? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
