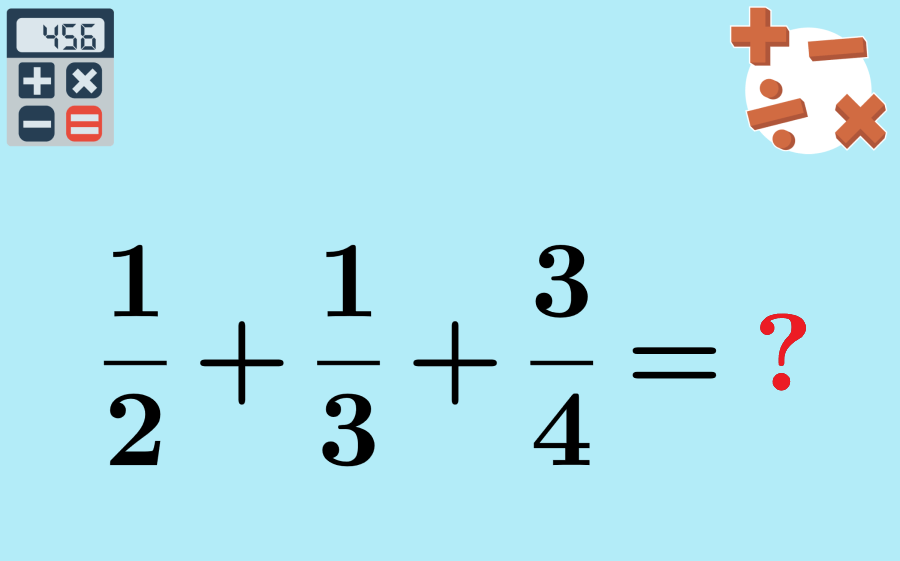We can add like fractions (with the same denominator) by adding the denominators and using the same denominator. On the other hand, unlike fractions (with different denominators) are added by finding their least common denominator. Then, we write equivalent fractions using that denominator and add their numerators.
Here, we will learn to add like and unlike fractions using step-by-step examples. In addition, you will be able to apply what you have learned with some practice problems.
10 Adding fractions examples with answers
The following examples are solved using the processes of solving the addition of like fractions and unlike fractions. Try to solve the problems yourself before looking at the solution.
EXAMPLE 1
Solve the addition of fractions $latex \frac{1}{5}+\frac{1}{5}$.
Solution
These fractions are like fractions since the denominator of both fractions is equal to 5.
Therefore, we can combine the fractions as follows:
$$\frac{1}{5}+\frac{1}{5}$$
$$=\frac{1+1}{5}$$
Adding the numerators, we have:
$$=\frac{1+1}{5}$$
$$=\frac{2}{5}$$
EXAMPLE 2
Find the result of the addition of fractions $latex \frac{2}{7}+\frac{3}{7}$.
Solution
These fractions are also like fractions since their denominators are equal to 7.
When we combine the fractions, we have:
$$\frac{2}{7}+\frac{3}{7}$$
$$=\frac{2+3}{7}$$
Adding the denominators, we have:
$$=\frac{2+3}{7}$$
$$=\frac{5}{7}$$
EXAMPLE 3
Find the result of the addition $latex \frac{1}{5}+\frac{2}{5}+\frac{1}{5}$.
Solution
In this case, we have an addition of three like fractions because the denominator of all three fractions equals 5.
Combining the fractions using a single denominator, we have:
$$\frac{1}{5}+\frac{2}{5}+\frac{1}{5}$$
$$=\frac{1+2+1}{5}$$
Adding the numerators, we have:
$$=\frac{1+2+1}{5}$$
$$=\frac{4}{5}$$
EXAMPLE 4
Solve the addition of fractions $latex \frac{2}{9}+\frac{4}{9}+\frac{7}{9}$.
Solution
All three fractions have the same denominator, so we have an addition of three like fractions.
Combining the fractions using a single denominator, we have:
$$\frac{2}{9}+\frac{4}{9}+\frac{7}{9}$$
$$=\frac{2+4+7}{9}$$
Adding the numerators, we have:
$$=\frac{2+4+7}{9}$$
$$=\frac{13}{9}$$
We can simplify the fraction by writing it as a mixed number:
$$=1\frac{4}{9}$$
EXAMPLE 5
Find the result of the addition $latex \frac{2}{3}+\frac{1}{4}$.
Solution
In this case, we have an addition of unlike fractions since their denominators are different. Therefore, we start by finding the least common denominator (LCD). The LCD of 3 and 4 is 12.
Dividing 12 by 3 (denominator of the first fraction), we get 4. Dividing 12 by 4 (denominator of the second fraction), we get 3.
Now, we multiply both the numerator and the denominator of each fraction by the numbers obtained in the previous step, 4 for the first fraction and 3 for the second:
$$\frac{2\times 4}{3 \times 4}+\frac{1 \times 3}{4 \times 3}$$
$$=\frac{8}{12}+\frac{3}{12}$$
Now that we have like fractions, we can add as follows:
$$\frac{8}{12}+\frac{3}{12}$$
$$=\frac{8+3}{12}$$
$$=\frac{11}{12}$$
EXAMPLE 6
What is the result of the addition $latex \frac{3}{4}+\frac{2}{5}$?
Solution
We have unlike fractions, so we start by finding the least common denominator. The LCD of 4 and 5 is 20.
Dividing 20 by 4 (denominator of the first fraction), we get 5. Dividing 20 by 5 (denominator of the second fraction), we get 4.
Now, we multiply the numerators and denominators by the numbers obtained in the previous step, 5 for the first fraction and 4 for the second:
$$\frac{3\times 5}{4 \times 5}+\frac{2 \times 4}{5 \times 4}$$
$$=\frac{15}{20}+\frac{8}{20}$$
Adding the like fractions, we have:
$$\frac{15}{20}+\frac{8}{20}$$
$$=\frac{15+8}{20}$$
$$=\frac{23}{20}$$
We can simplify by writing as a mixed number:
$$=1\frac{3}{20}$$
EXAMPLE 7
Solve the addition $latex \frac{1}{3}+\frac{1}{4}+\frac{1}{2}$.
Solution
We have a sum of three unlike fractions, so we need to find the LCD. The LCD of 3, 4, and 2 is 12.
Dividing 12 by 3 (first denominator), we get 4. Dividing 12 by 4 (second denominator), we get 3. Dividing 12 by 2 (third denominator), we get 6.
Now, we are going to multiply the numerators and denominators of each fraction by the numbers obtained in the previous step, 4 for the first fraction, 3 for the second, and 6 for the third:
$$\frac{1\times 4}{3 \times 4}+\frac{1 \times 3}{4 \times 3}+\frac{1 \times 6}{2 \times 6}$$
$$=\frac{4}{12}+\frac{3}{12}+\frac{6}{12}$$
Solving the addition of like fractions from the previous step, we have:
$$\frac{4}{12}+\frac{3}{12}+\frac{6}{12}$$
$$=\frac{4+3+6}{12}$$
$$=\frac{13}{12}$$
We can simplify by writing as a mixed number:
$$=1\frac{1}{12}$$
EXAMPLE 8
Find the result of the addition $latex \frac{2}{5}+\frac{3}{4}+\frac{1}{2}$.
Solution
Since we have unlike fractions, we start by finding the LCD. The LCD of 5, 4, and 2 is 20.
Dividing 20 by 5 (first denominator), we get 4. Dividing 20 by 4 (second denominator), we get 5. Dividing 20 by 2 (third denominator), we get 10.
Now, we multiply both the numerator and denominator of each fraction by the numbers obtained in the previous step, 4 for the first fraction, 5 for the second, and 10 for the third:
$$\frac{2\times 4}{5 \times 4}+\frac{3 \times 5}{4 \times 5}+\frac{1 \times 10}{2 \times 10}$$
$$=\frac{8}{20}+\frac{15}{20}+\frac{10}{20}$$
Solving the addition of like fractions obtained, we have:
$$\frac{8}{20}+\frac{15}{20}+\frac{10}{20}$$
$$=\frac{8+15+10}{20}$$
$$=\frac{33}{20}$$
We can simplify by writing as a mixed number:
$$=1\frac{13}{20}$$
EXAMPLE 9
Solve the addition $latex \frac{2}{3}+\frac{1}{3}+\frac{2}{7}+\frac{3}{7}$.
Solution
The denominators of the first two fractions are equal to 3 and the denominators of the last two fractions are 7. Thus, the least common denominator is 21.
Dividing 21 by 3 (first and second denominators), we get 7. Dividing 21 by 7 (third and fourth denominators), we get 3.
Now, we are going to multiply both the numerators and the denominators of each fraction by the numbers obtained in the previous step, 7 for the first two fractions and 3 for the last two:
$$\frac{2\times 7}{3 \times 7}+\frac{1 \times 7}{3 \times 7}+\frac{2 \times 3}{7 \times 3}+\frac{3 \times 3}{7 \times 3}$$
$$=\frac{14}{21}+\frac{7}{21}+\frac{6}{21}+\frac{9}{21}$$
Solving this addition of like fractions, we have:
$$\frac{14}{21}+\frac{7}{21}+\frac{6}{21}+\frac{9}{21}$$
$$=\frac{14+7+6+9}{21}$$
$$=\frac{36}{21}$$
Simplifying and writing as a mixed number, we have:
$$=\frac{12}{7}$$
$$=1\frac{5}{7}$$
EXAMPLE 10
Solve the addition $latex \frac{3}{4}+\frac{2}{3}+\frac{4}{5}+\frac{1}{2}$.
Solution
We start by finding the LCD of the fractions. The LCD of 4, 3, 5, and 2 is 60.
Dividing 60 by 4 (first denominator), we get 15. Dividing 60 by 3 (second denominator), we get 20. Dividing 60 by 5 (third denominator), we get 12. Dividing 60 by 2, we get 30.
We multiply the numerators and denominators of each fraction by the numbers obtained in the previous step, 15 for the first fraction, 20 for the second, 12 for the third, and 30 for the fourth:
$$\frac{3\times 15}{4 \times 15}+\frac{2 \times 20}{3 \times 20}+\frac{4 \times 12}{5 \times 12}+\frac{1 \times 30}{2 \times 30}$$
$$=\frac{45}{60}+\frac{40}{60}+\frac{48}{60}+\frac{30}{60}$$
Now that we have an addition of like fractions, we can easily solve it:
$$\frac{45}{60}+\frac{40}{60}+\frac{48}{60}+\frac{30}{60}$$
$$=\frac{45+40+48+30}{60}$$
$$=\frac{163}{60}$$
We can simplify by writing as a mixed number:
$$=2\frac{43}{60}$$
5 Adding fractions practice problems
Solve the following problems to practice the process used to add both like and unlike fractions.
See also
Interested in learning more about adding fractions? You can take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
