A logarithmic scale is a non-linear scale that is frequently used to analyze data that vary over a very large range. By using this scale, each interval is increased by a factor that is equal to the base of the logarithm, instead of increasing in equal increments. Typically, base-10 or base-e scales are used.
Logarithmic scales are useful for various applications, some of which are the pH scale used in chemistry to analyze acidic substances or bases, the decibel scale used to measure sound, and the Richter scale used to measure the intensity of the earthquakes.
Uses of logarithmic scales
Because logarithmic scales grow very slowly, they are useful for modeling situations where we have a very wide range of values. For example, bacteria can grow very quickly. Under ideal conditions, bacteria can divide in as little as 30 minutes, and those bacteria divide again in 30 minutes.
If this process began with a single bacterium, the exponential growth of the bacteria would produce almost 17 million bacteria in just 12 hours. The following graph illustrates this growth:
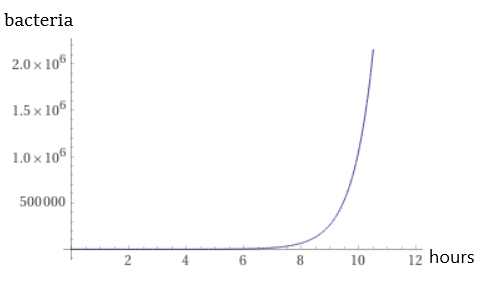
This is a good graph, but it has a problem. Each axis on the graph uses a linear scale, so even though the information is accurately represented, it is very difficult to know what is happening with the growth of the bacteria until about the 8-hour point.
We need a way to rescale one of the axes so that all the information can be used. This is why logarithmic scales were developed.
Recall that a logarithm is simply the power to which the base has to be raised to obtain a particular number. The definition of a logarithmic scale is that it is a scale in which the units on the axes are powers or logarithms and are typically used when the increase or decrease in value on that axis is exponential.
In most cases, the base used is 10. If only one axis uses a logarithmic scale, then it is called a semi-log graph. If both axes use a logarithmic scale, then it is called a log-log graph.
In order to obtain more information from the graph of the growth of bacteria, we can change one of the axes with a linear scale to a logarithmic scale and form a semi-log graph. We are going to reformat the y-axis using powers of 10 to represent the growth of bacteria:
Now, instead of the linear y-axis, each unit is a power of 10. For example, the first number is 0 and $latex {{10}^0}$ represents 1. Then, we have $latex {{10}^1}=10$. Then, $latex {{10}^2}=100$ and so on.
By doing this, we have created a graph that is a straight line and it is easier to get information like this. For example, the value of the logarithm in 4 hours is around 2.4. 10 to the power of 2.4 is 251 bacteria.
pH scale
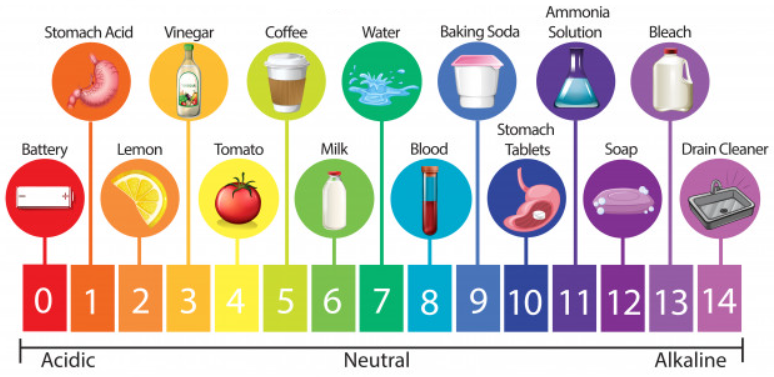
An example of the common use of logarithmic scales is the pH scale. The pH scale is used in chemistry to measure the acidity of a substance or chemical compound. This scale is based on the concentration of hydrogen ions in the substance, denoted by $latex [H^{+}]$. The pH value is defined by the formula:
$latex pH = – \log_{10}[{{H}^{+}}]$
PH values range from 0 to 14, where 7 indicates a neutral solution. The lower the pH level, the more acidic the substance. The following are some common substances with their pH values:
EXAMPLE 1
- Calculate the pH of a solution that has a hydrogen ion concentration of $latex 3.98\times {{10}^{-5}}$.
Solution: We can use the calculator and the formula to calculate the pH of a substance with $latex [{{H}^{+}}]=3.98\times {{10}^{-5}}$:
$latex pH=-\log_{10}(3.98\times {{10}^{-5}})=4.4$
EXAMPLE 2
- The water in a container has a pH of 7.5. What is its hydrogen ion concentration?
Solution: In this case, we have to solve the equation:
$latex 7.5=-\log_{10}[{{H}^{+}}]$
We can rewrite as follows:
$latex -7.5=\log_{10}[{{H}^{+}}]$
Now, we convert the equation to its exponential form:
$latex [{{H}^{+}}]={{10}^{-7.5}}\approx 3.2\times {{10}^{-8}}$
The hydrogen ion concentration of water is $latex 3.2\times {{10}^{-8}}$.
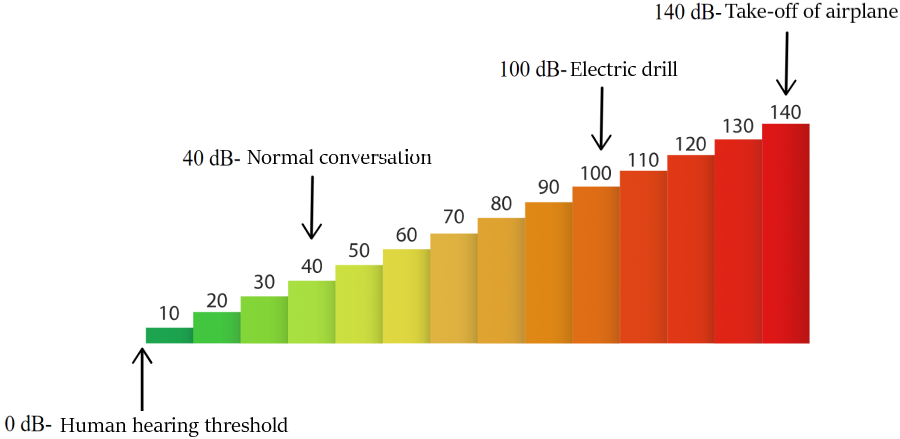
Decibel scale
Another example of a logarithmic scale is the decibel scale that is used to measure the intensity of sound. The volume of sound is measured in decibels, d, using the following formula:
$latex dB=10\log_{10}(\frac{I}{{{10}^{-12}}})$
where $latex I$ is the intensity of sound waves measured in watts per square meter. For example, the intensity of a whisper is equal to $latex {{10}^{-10}}\frac{watts}{{{m}^2}}$ and the intensity of thunder is equal to $latex {{10}^{-1}}\frac{watts}{{{m}^2}}$.
If we always used these units, we would have very large differences between the measurements. In this case, we have:
$latex \frac{\text{intensity thunder}}{\text{intensy whisper}}=\frac{{{10}^{-1}}}{{{10}^{-10}}}={{10}^9}$
Thunder is $latex {{10}^9}$ or a million times louder than a whisper. It would be very difficult to compare such different sounds. However, on the decibel scale, a whisper equals 20 decibels and a thunderbolt equals 110 decibels. This is much simpler.
EXAMPLE
- Breathing normally generates around $latex {{10}^{-11}}$ watts per square meter at a distance of 1 meter. What is the equivalence in decibels?
Solution: We use the decibel formula with $latex I={{10}^{-11}}$:
$latex dB=10\log_{10}(\frac{{{10}^{-11}}}{{{10}^{-12}}})=0\log_{10}({{10}^1}})$
$latex =10(1)=10$ decibels
Richter scale
The Richter scale is a method of measuring the magnitude of an earthquake. This scale compares the amplitude of the seismographic wave with the amplitude of the wave produced by the smallest detectable earthquake, $latex A_{0}$. The logarithm of the quotient of these amplitudes is equal to the Richter scale, M. Therefore, we have:
$latex M = \log_{10}(\frac{A}{A_{0}})$
EXAMPLE
- What would be the magnitude of an earthquake 100 times stronger than a 6.9 earthquake on the Richter scale?
Solution: We can use $latex A_{a}$ to represent the amplitude of the earthquake waves that have 6.9 on the Richter scale and we can represent with $latex A_{b}$ the amplitude of the earthquake waves that is 100 times stronger. From the formula of the Richter scale, we have:
$latex 6.9=\log_{10}(\frac{A_{a}}{A_{0}})$
Now, we can write this in exponential form:
$latex \frac{A_{a}}{A_{0}}={{10}^{6.9}}$
We know that $latex A_{b}=100A_{a}$, so we have:
$latex \frac{A_{a}}{A_{0}}=\frac{100A_{b}}{A_{0}}$
$latex =100(\frac{A_{b}}{A_{0}})$
$latex ={{10}^2}({{10}^{6.9}})$
$latex ={{10}^{8.9}}$
Thus, the magnitude of the stronger earthquake is:
$latex \log_{10}(\frac{A_{a}}{A_{0}})=\log_{10}({{10}^{8.9}})$
$latex =8.9$
See also
Interested in learning more about logarithmic equations? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
