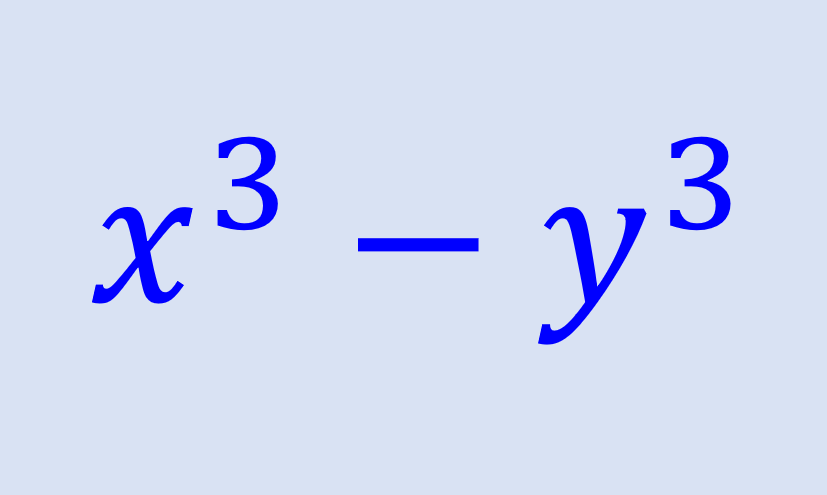A polynomial of the form a³-b³ is called a difference of cubes. These types of polynomials can be easily factored using a standard pattern. Here, we will learn the process used to factor a difference of cubes.
We will look at several examples with answers to fully master the topic of factoring difference of cubes.
How to factor a difference of cubes?
To factor a difference of cubes, we can follow the following steps:
Step 1: Decide if the two terms have a common factor, called the greatest common factor. If so, we factor the greatest common factor from the expression. We must not forget to include the greatest common factor as part of the final answer.
Step 2: Rewrite the original problem as a difference of two perfect cubes.
Step 3: Use the following sentences to write the answer:
a) “Write what you see”
b) “Square – Multiply – Square”
c) “Negative, Positive, Positive”
Step 4: Use all three parts to write the final answer.
Factoring a difference of cubes – Examples with answers
The following difference of cubes factoring examples use the solving process listed above. Each example has a detailed solution that helps to understand the reasoning used to obtain the answer.
EXAMPLE 1
Factor the expression $latex {{x}^3}-8$.
Solution
Step 1: In this case, the terms do not have any common factors, so we cannot factor initially.
Step 2: We rewrite the original problem as a difference of two perfect cubes:
⇒ $latex {{(x)}^3}-{{(2)}^3}$
Step 3: a) If we remove the parentheses and ignore the cubes, we see the expression:
$latex x-2$
b) If we square the first term, x, we have $latex {{x}^2}$. If we multiply the terms x and 2, we have $latex 2x$. If we square the second term, 2, we have 4.
$latex {{x}^2},~~2x,~~4$
c) “Negative, Positive, Positive”. These are the signs of the problem.
Step 4: The final answer is:
$latex (x-2)({{x}^2}+2x+4)$
EXAMPLE 2
Factor the expression $latex 8{{x}^3}-27$.
Solution
Step 1: We have no common factors in the terms, so we cannot factor initially.
Step 2: We have to rewrite the original problem as a difference of two perfect cubes:
⇒ $latex {{(2x)}^3}-{{(3)}^3}$
Step 3: a) Ignoring the parentheses and cubes, we see the expression:
$latex 2x-3$
b) Squaring the first term, x, we have $latex 4{{x}^2}$. Multiplying the terms 2x and 3, we have $latex 6x$. Squaring the second term, 3, we have 9.
$latex 4{{x}^2},~~6x,~~9$
c) “Negative, Positive, Positive”. These are the signs of the problem.
Step 4: The final answer is:
$latex (2x-3)(4{{x}^2}+6x+9)$
EXAMPLE 3
Obtain the factorization of $latex 27{{x}^3}-125$.
Solution
Step 1: This expression also cannot be factored initially since there are no common factors in the terms.
Step 2: We rewrite the original problem as a difference of two perfect cubes:
⇒ $latex {{(3x)}^3}-{{(5)}^3}$
Step 3: a) Ignoring the parentheses and cubes, we see the expression:
$latex 3x-5$
b) Squaring the first term, 3x, we have $latex 9{{x}^2}$. By multiplying the terms 3x and 5, we have$latex 15x$. Squaring the second term, 5, we have 25.
$latex 9{{x}^2},~~15x,~~25$
c) “Negative, Positive, Positive”. These are the signs of the problem.
Step 4: The factored version is:
$latex (3x-5)(9{{x}^2}+15x+25)$
EXAMPLE 4
Factor the expression $latex 125{{x}^3} -216{{y}^3}$.
Solution
Step 1: The terms do not have any common factors, so we continue with the following steps.
Step 2: We write the original expression as a difference of two perfect cubes:
⇒ $latex {{(5x)}^3}-{{(6y)}^3}$
Step 3: a) If we ignore the parentheses and cubes, we see the expression:
$latex 5x-6y$
b) We square the first term, 5x, to get $latex 25{{x}^2}$. We multiply the terms 5x and 6y, to get $latex 30xy$. We square the second term, 6y, to obtain $latex 36{{y}^2}$.
$latex 25{{x}^2},~~30xy,~~36{{y}^2}$
c) “Negative, Positive, Positive”. These are the signs of the problem.
Step 4: The final answer is:
$latex (5x-6y)(25{{x}^2}+30xy+36{{y}^2})$
EXAMPLE 5
Obtain the factorization of the expression $latex 54{{x}^3}-16{{y}^3}$.
Solution
Step 1: This expression does have common factors. We can extract the 2 from both terms:
$latex 2(27{{x}^3}-8{{y}^3})$
Step 2: We rewrite the expression obtained as a difference of two perfect cubes:
⇒ $latex 2({{(3x)}^3}-{{(2y)}^3})$
Step 3: a) By removing the parentheses and ignoring the cubes, we have:
$latex 3x-2y$
b) If we square the first term, 3x, we have $latex 9{{x}^2}$. If we multiply the terms 3x and 2y, we have $latex 6xy$. If we square the second term, 2y, we have $latex 4{{y}^2}$.
$latex 9{{x}^2},~~6xy,~~4{{y}^2}$
c) “Negative, Positive, Positive”. These are the signs of the problem.
Step 4: We obtained the following factorization:
$latex 2(3x-2y)(9{{x}^2}+6xy+4{{y}^2})$
EXAMPLE 6
Factor the expression $latex 1-125{{x}^3}{{y}^3}$.
Solution
Step 1: We have no common factors.
Step 2: By rewriting the expression as a difference of two perfect cubes, we have:
⇒ $latex {{(1)}^3}-{{(5xy)}^3}$
Step 3: a) If we remove the parentheses and ignore the cubes, we see the expression:
$latex 1-5xy$
b) Squaring the first term, 1, we have 1. Multiplying the terms 1 and 5xy, we get $latex 5xy$. Squaring the second term, 5xy, we have $latex 25{{x}^2}{{y}^2}$.
$latex 1,~~5xy,~~25{{x}^2}{{y}^2}$
c) “Negative, Positive, Positive”. These are the signs of the problem.
Step 4: The final answer is:
$latex (1-5xy)(1+5xy+25{{x}^2}{{y}^2})$
Factoring difference of cubes – Practice problems
Test what you have learned about factoring the difference of cubes with the following problems. Solve the exercises and choose an answer. Check the selected answer to see if it is correct.
See also
Interested in learning more about the factorization of polynomials? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
