Polynomials are algebraic expressions that contain variables and coefficients along with mathematical operations such as addition, subtraction, and multiplication. We can perform mathematical operations similar to how we perform operations with algebraic expressions.
Here, we will look at a summary of polynomials and their mathematical operations. Then, we will look at several solved polynomial exercises to learn how to perform these operations with polynomials.
Summary of polynomials
Polynomials are algebraic expressions consisting of variables, constants, and exponents that are combined using mathematical operations such as addition, subtraction, and multiplication.
Based on the number of terms in the expression, polynomials can be classified as monomial, binomial, trinomial, and others. The following are examples of variables, constants, and exponents:
- Constants: 1, 2, 3, etc.
- Variables: a, b, x, y, etc.
- Exponents: the 2 in $latex {{x}^2}$.
A polynomial function is usually represented by $latex P(x)$, where x is the variable.
We can perform various mathematical operations with polynomials. Let’s look at a summary of addition, subtraction, and multiplication of polynomials.
Adding polynomials
To add polynomials, we simply have to combine like terms. Remember that like terms are terms that have the same variables raised to the same powers.
The addition of polynomials always results in a polynomial of the same degree.
Polynomial subtraction
Polynomial subtraction is similar to addition with the difference that we have a change of signs. Therefore, we subtract the like terms to get the solution.
Polynomial subtraction also results in a polynomial of the same degree.
Multiplication of polynomials
To multiply polynomials, we have to use the distributive property to multiply all terms. The distributive property is:
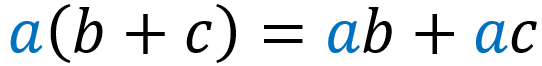
When we multiply two or more polynomials, we always get a polynomial with a larger degree, unless one of the polynomials is a constant.
Exercises with answers of polynomials
The following exercises detail the process used to perform mathematical operations with polynomials. Try to solve the exercises yourself before looking at the answer.
EXERCISE 1
Find the result of the addition: $latex (4{{x}^2}+5)+(3{{x}^2}+4)$.
Solution
To add the polynomials, we have to combine like terms. Therefore, we combine the terms with $latex {{x}^2}$ and the constant terms separately:
$latex (4{{x}^2}+5)+(3{{x}^2}+4)$
$latex =7{{x}^2}+9$
EXERCISE 2
Find the result of the subtraction of polynomials: $latex (2{{x}^3}+4{{x}^2}+4)-(3{{x}^3}+2{{x}^2}+2)$.
Solution
In this case, we have to subtract the like terms. We compare all the terms that are similar:
$latex (2{{x}^3}+4{{x}^2}+4)-(3{{x}^3}+2{{x}^2}+2)$
$latex =2{{x}^3}-3{{x}^3}+4{{x}^2}-2{{x}^2}+4-2$
$latex =-{{x}^3}+2{{x}^2}+2$
EXERCISE 3
Find the result of the addition of polynomials: $latex (3{{x}^5}+8{{x}^4}-4{{x}^3}+2{{x}^2}-5x+2)$ $latex +(4{{x}^5}-4{{x}^4}-2{{x}^3}+5{{x}^2}+3x+10)$.
Solution
In this case, we have several terms with different variables and different signs. However, we have to apply the same idea. We identify like terms and combine them:
$latex (3{{x}^5}+8{{x}^4}-4{{x}^3}+2{{x}^2}-5x+2)$ $latex +(4{{x}^5}-4{{x}^4}-2{{x}^3}+5{{x}^2}+3x+10)$
$latex =7{{x}^5}+4{{x}^4}-6{{x}^3}+7{{x}^2}-2x+12$
EXERCISE 4
Find the result of the subtraction of polynomials: $latex (2{{x}^5}y+4{{x}^4}-3{{x}^3}+5{{x}^2}y-5x+2)$ $latex -(6{{x}^5}-4{{x}^4}+2{{x}^3}+2{{x}^2}+3x-5)$.
Solution
This polynomial has terms with the variable y, which do not have like terms. Therefore, we have to combine only the like terms and just copy the terms that have no like terms:
$$(2{{x}^5}y+4{{x}^4}-3{{x}^3}+5{{x}^2}y-5x+2) -(6{{x}^5}-4{{x}^4}+2{{x}^3}+2{{x}^2}+3x-5)$$
$$=2{{x}^5}y-6{{x}^5}+(4+4){{x}^4}+(-3-2){{x}^3} +5{{x}^2}y-2{{x}^2}+(-5-3)x+2+5$$
$$=2{{x}^5}y-6{{x}^5}+8{{x}^4}-5{{x}^3}+5{{x}^2}y-2{{x}^2}-8x+7$$
EXERCISE 5
Find the result of the multiplication: $latex (4x+2)(3x-3)$.
Solution
We have to use the distributive property to distribute and multiply all the terms. Therefore, we have:
$latex (4x+2)(3x-3)$
$latex =4x(3x-3)+2(2x-3)$
$latex =12{{x}^2}-12x+4x-6$
Now, we just have to combine like terms to simplify:
$latex =12{{x}^2}-12x+4x-6$
$latex =12{{x}^2}-8x-6$
EXERCISE 6
Multiply the polynomials: $latex (2{{x}^2}+5x)(4{{x}^2}-2x+3)$.
Solution
Again, we use the distributive property to multiply all the terms of the polynomial. Then, we simplify the result by combining like terms:
$latex (2{{x}^2}+5x)(4{{x}^2}-2x+3)$
$$=2{{x}^2}(4{{x}^2}-2x+3)+5x(4{{x}^2}-2x+3)$$
$$=8{{x}^4}-4{{x}^3}+6{{x}^2}+20{{x}^3}-10{{x}^2}+15x$$
$latex =8{{x}^4}+16{{x}^3}-4{{x}^2}+15x$
EXERCISE 7
Find the product of the multiplication: $latex (5x^2-3x+2)(2x^2+4x-5)$.
Solution
Similar to the previous exercises, we have to use the distributive property to multiply all the terms. Then we simplify the result by combining like terms:
$latex (5x^2-3x+2)(2{{x}^2}+4x-5)$
$$=5x^2(2{{x}^2}+4x-5)-3x(2{{x}^2}+4x-5) +2(2{{x}^2}+4x-5)$$
$$=10{{x}^4}+20{{x}^3}-25{{x}^2}-6{{x}^3}-12{{x}^2} +15x+4{{x}^2}+8x-10$$
$latex =10{{x}^4}+14{{x}^3}-33{{x}^2}+23x-10$
Polynomials – Practice problems
Put into practice your knowledge about polynomials and your skills to solve operations with polynomials with the following problems. If you need help, you can look at the solved exercises above.
See also
Interested in learning more about algebraic topics? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
