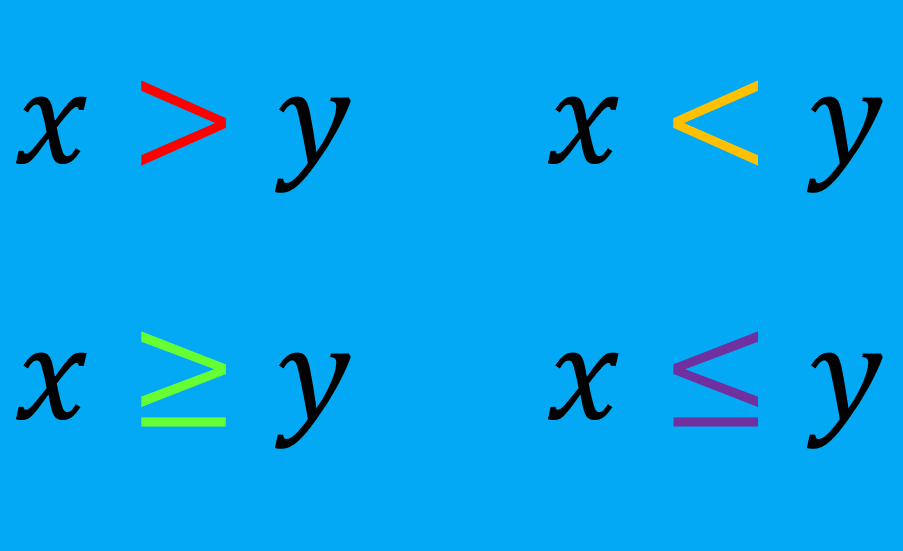Inequality problems and exercises can be solved with a process similar to the one we use to solve equations. The main difference regarding inequalities is that we have to change the side of the inequality sign when we multiply or divide by negative numbers.
Here, we will look at a summary of how to solve inequalities. In addition, we will look at several examples with answers to master the process of solving inequalities.
Process used to solve inequalities
Remember that inequalities are relationships that compare two values using the signs greater than (>), less than (<), greater than or equal to (≥), and less than or equal to (≤). For example, $latex 3x<6$ and $latex 2x+2>3$ are inequalities.
To solve inequalities, we can follow the following steps:
Step 1: We simplify the inequality if possible. This includes removing grouping signs such as parentheses, combining like terms, and removing fractions.
Step 2: Solve for the variable. We have to do addition and subtraction so that all the variables are located on one side of the inequality and the constants are located on the other side.
Step 3: Solve. We use division or multiplication to find the answer. Note: When we multiply or divide an inequality by a negative number, we must switch sides to the inequality sign.
Step 4: If we have to graph, we have to remember that we use an empty point to indicate that the limiting number is not part of the solution and we use a filled point to indicate that the limiting number is part of the solution.
For example, if the solution is $latex x>2$, the 2 is not part of the solution, so we use an empty point and if the solution is $latex x \ge 2$, the 2 is part of the solution, so we use a filled point.
Inequalities – Examples with answers
EXAMPLE 1
Solve and graph the inequality $latex 3x-5>1$.
Solution
- We start by writing the original problem:
$latex 3x-5>1$
- To solve for the variable, we add 5 to both sides of the inequality:
$latex 3x-5+5>1+5$
- After simplifying, the expression reduces to:
$latex 3x>6$
- To solve, we divide both sides by 3:
$latex \frac{3}{3}x> \frac{6}{3}$
$latex x> 2$
- We graph the inequality with an open point since 2 is not included in the solution. The solution is all the numbers to the right of 2:
EXAMPLE 2
Solve and graph the inequality $latex 5x-10<15$.
Solution
Step 1: Here, we have nothing to simplify, so we start with:
$latex 5x-10<15$
Step 2: To solve for the variable, we add 10 from both sides and simplify:
$latex 5x-10+10<15+10$
$latex 5x<25$
Step 3: To solve, we divide both sides by 5:
$latex \frac{5}{5}x<\frac{25}{5}$
$latex x<5$
Step 4: To graph, we note that the solutions to the inequality are all real numbers to the left of 5. The 5 is not included, so we use an empty point to indicate this:
EXAMPLE 3
Solve and graph the inequality $latex -4x-5\leq 3$.
Solution
Step 1: We have nothing to simplify, so we start with:
$latex -4x-5\leq 3$
Step 2: We add 5 to both sides to solve for the variable:
$latex -4x-5+5\leq 3+5$
$latex -4x\leq 8$
Step 3: We divide both sides by -4 to get:
$latex \frac{-4}{-4}x\leq\frac{8}{-4}$
$latex x\geq -2$
| Don’t forget to change the inequality sign when multiplying or dividing by a negative number. |
Step 4: In this case, -2 is part of the solution. Therefore, we use a solid point to indicate that the solutions are all numbers to the right of -2, including -2:
EXAMPLE 4
Solve and graph the inequality $latex 4x+2\geq 2x+10$.
Solution
In this case, we have variables on both sides. We have to move the variables to one side and the constants to the other. It doesn’t matter which side contains the variables, but it is common to move the variables to the left:
- We start with the original problem:
$latex 4x+2\geq 2x+10$
- We subtract 2 and 2x from both sides to solve for the variable:
$$4x+2-2-2x\geq 2x+10-2-2x$$
- Simplifying the inequality, we have:
$latex 2x\geq 8$
- We divide both sides by 2 and simplify to get the answer:
$latex \frac{2}{2}x\geq \frac{8}{2}$
$latex x\geq 4$
- Here, the 4 is part of the solution, so we use a closed point to indicate this:
EXAMPLE 5
Solve the inequality $latex 5x+3>3x-3$.
Solution
Step 1: We have nothing to simplify. We start with the inequality:
$latex 5x+3>3x-3$
Step 2: We subtract 3 and 3x from both sides to solve for the variable:
$latex 5x+3-3-3x>3x-3-3-3x$
$latex 2x>-6$
Step 3: We divide both sides by 2 to solve:
$latex \frac{2}{2}x>\frac{-6}{2}$
$latex x>-3$
EXAMPLE 6
Solve the inequality $latex 3(x+2)>-9$.
Solution
Step 1: We have parentheses, so we apply the distributive property to eliminate them:
$latex 3(x+2)>-9$
$latex 3x+6>-9$
Step 2: To solve for the variable, we subtract 6 from both sides:
$latex 3x+6-6>-9-6$
$latex 3x>-15$
Step 3: To solve, we divide both sides by 3:
$latex \frac{3}{3}x>\frac{-15}{3}$
$latex x>-5$
EXAMPLE 7
Solve the inequality $latex 2(3x-3)>4x$.
Solution
In this case, we have parentheses, so we use the distributive property to remove parentheses and simplify:
- We write the original problem:
$latex 2(3x-3)>4x$
- We apply the distributive property:
$latex 2(3x)+2(-3)>4x$
$latex 6x-6>4x$
- We add 6 from both sides and subtract 4x to solve for the variable:
$$6x-6+6-4x>4x+6-4x$$
- After simplifying, the expression reduces to:
$latex 2x>6$
- By dividing both sides by 2, we have:
$latex \frac{2}{2}x> \frac{6}{2}$
$latex x> 3$
EXAMPLE 8
Solve the inequality $latex 2(2x+4)+5>1$.
Solution
Step 1: We simplify the parentheses and combine like terms:
$latex 2(2x+4)+5>1$
$latex 4x+8+5>1$
$latex 4x+13>1$
Step 2: We isolate the variable by subtracting 13 from both sides:
$latex 4x+13-13>1-13$
$latex 4x>-12$
Step 3: We have to divide by 4:
$latex \frac{4}{4}x>\frac{-12}{4}$
$latex x>-3$
EXAMPLE 9
Solve the inequality $latex 4(2x+4)-3\leq 2(3x+4)+3$.
Solution
Step 1: We simplify the parentheses on both sides and combine like terms:
$latex 4(2x+4)-3\leq 2(3x+4)+3$
$latex 8x+16-3\leq 6x+8+3$
$latex 8x+13\leq 6x+11$
Step 2: We subtract 13 and 6x from both sides to solve for the variable:
$$8x+13-13-6x\leq 6x+11-13-6x$$
$latex 2x\leq -2$
Step 3: To solve, we divide both sides by 2:
$latex \frac{2}{2}x\leq \frac{-2}{2}$
$latex x\leq -1$
EXAMPLE 10
Solve the inequality $latex 2(x+5)-10\geq 4(2x+6)$.
Solution
Step 1: We simplify the parentheses on both sides and combine like terms:
$latex 2(x+5)-10\geq 4(2x+6)$
$latex 2x+10-10\geq 8x+24$
$latex 2x\geq 8x+24$
Step 2: We subtract both sides by 8x to solve for x:
$latex 2x-8x\geq 8x+24-8x$
$latex -6x\geq 24$
Step 3: Now, we divide by -6:
$latex \frac{-6}{-6}x\geq\frac{24}{-6}$
$latex x\leq -4$
Inequalities – Practice problems
Solve the inequality $latex (-3x-2)+2>-x-2(-2x+6)$
Write the answer in the input box.
See also
Interested in learning more about inequalities? Take a look at these pages:
Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.
